Turing Machines¶
Related:
- Turing Machines
- Post systems
- mu-recursive functions
- lambda calc
- combinatory logic
Is it possible to write a program, that given the description of a machine M and an input for M, simulates the execution of the machine on that input? (spoilers: yes, with TMs)
Definition¶
- infinite tape
- but input is finite, rest of tape is blank
- scanning head
- can read cell from tape
- can write to tape
- finite control
- accept/reject
- tape alphabet
- always includes a special blank symbol, and the input alphabet
- input alphabet
- transition function
- inputs: (current state, symbol at head)
- outputs: (new state, symbol to write, move l/r)
- stop in accept or reject state

Formally:
- \(M = (Q, \Sigma, \Gamma, \delta, q_0, q_{acc}, q_{rej})\)

You can notate the current state of the machine and tape like this:

Examples¶
Note
The symbol for “empty” on the tape below is notated e.
Ex 1¶
Even length strings of 0s:
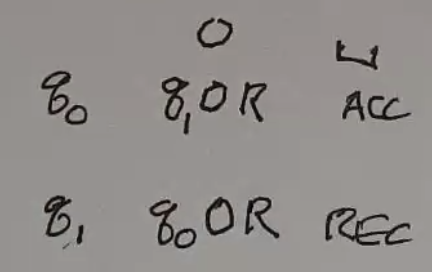
We can use some shorthand:
- If not changing states, omit new state
- If not writing, omit symbol to write
+----+------+-------+
| | 0 | e |
+====+======+=======+
| q0 | q1 R | ACC R |
+----+------+-------+
| q1 | q0 R | REJ r |
+----+------+-------+
Alternatively, you can use a state diagram:
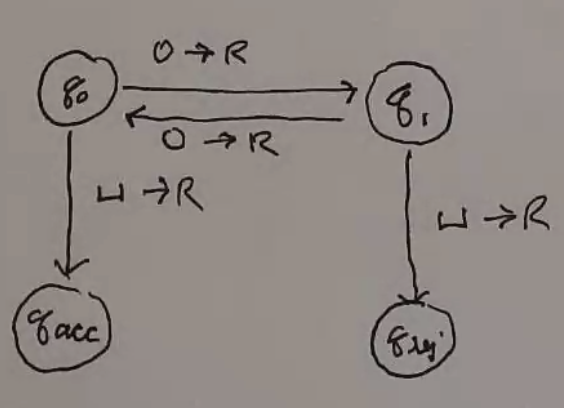
Ex 2¶
Even # of 0s, ignore 1s
+----+------+---+-----+
| | 0 | 1 | e |
+----+------+---+-----+
| q0 | q1 R | R | ACC |
+----+------+---+-----+
| q1 | q0 R | R | REJ |
+----+------+---+-----+
Ex 3¶
Add 1 to binary number
- \(\Sigma = \{0, 1\}\)
- \(\Gamma = \{>, 0, 1\}\)
Strategy: Move to the end of the tape, then go back and write 0s at each 1 until your carry is fine.
+----+-----+---------+-----+-------+
| | > | 0 | 1 | e |
+====+=====+=========+=====+=======+
| q0 | R | R | R | q1, L |
+----+-----+---------+-----+-------+
| q1 | REJ | ACC 1 L | 0 L | REJ |
+----+-----+---------+-----+-------+
Ex 4¶
Equal number of 0->1 transitions as 1->0 (assume string starts with 0)
+----+------+------+-----+
| | 0 | 1 | e |
+====+======+======+=====+
| q0 | R | q1 R | ACC |
+----+------+------+-----+
| q1 | q0 R | R | REJ |
+----+------+------+-----+
Ex 5¶
\(0^n1^n\)

+----+--------+--------+------+------+-----+
| | 0 | 1 | X | Y | e |
+====+========+========+======+======+=====+
| q0 | q1 X R | REJ | | q3 R | |
+----+--------+--------+------+------+-----+
| q1 | R | q2 Y L | REJ | R | REJ |
+----+--------+--------+------+------+-----+
| q2 | L | | q0 R | L | |
+----+--------+--------+------+------+-----+
| q3 | REJ | REJ | REJ | R | ACC |
+----+--------+--------+------+------+-----+
Execution looks like this:
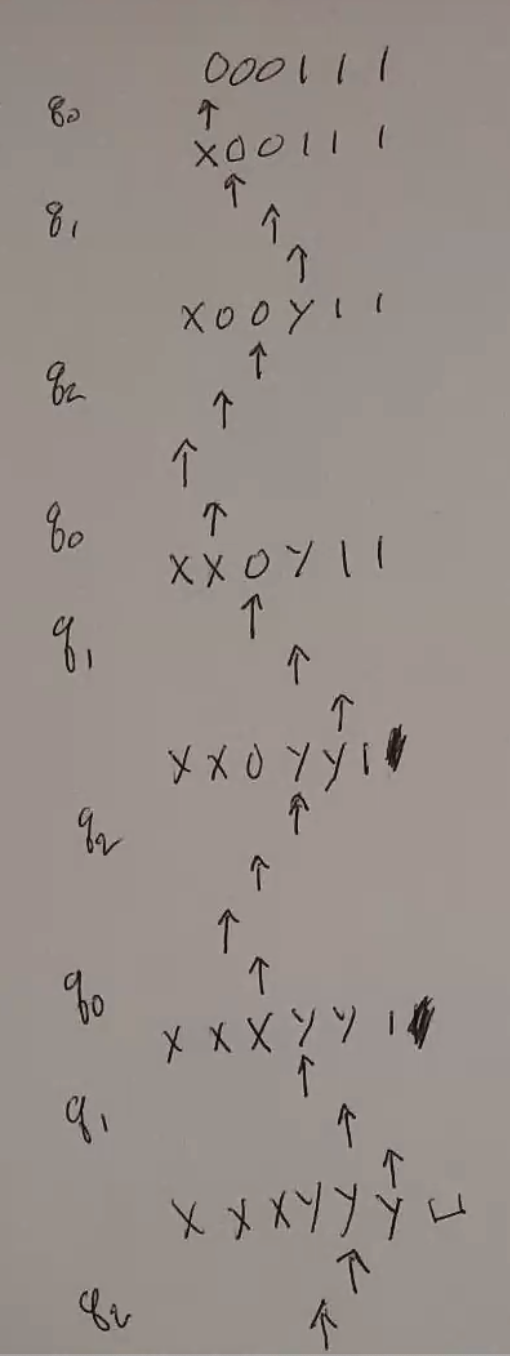
(con’t)

Ex 6¶
Palindromes
- \(\Gamma = \{>, 0, 1, e\}\)
- A string may look like
>010e.
+-----+--------+--------+-----+-------+
| | 0 | 1 | > | e |
+=====+========+========+=====+=======+
| s | q0 > R | q1 > R | R | ACC |
+-----+--------+--------+-----+-------+
| q0 | R | R | | q0' L |
+-----+--------+--------+-----+-------+
| q0' | q2 e L | REJ | ACC | |
+-----+--------+--------+-----+-------+
| q1 | R | R | | q1' L |
+-----+--------+--------+-----+-------+
| q1' | REJ | q2 e L | ACC | |
+-----+--------+--------+-----+-------+
| q2 | L | L | s R | |
+-----+--------+--------+-----+-------+
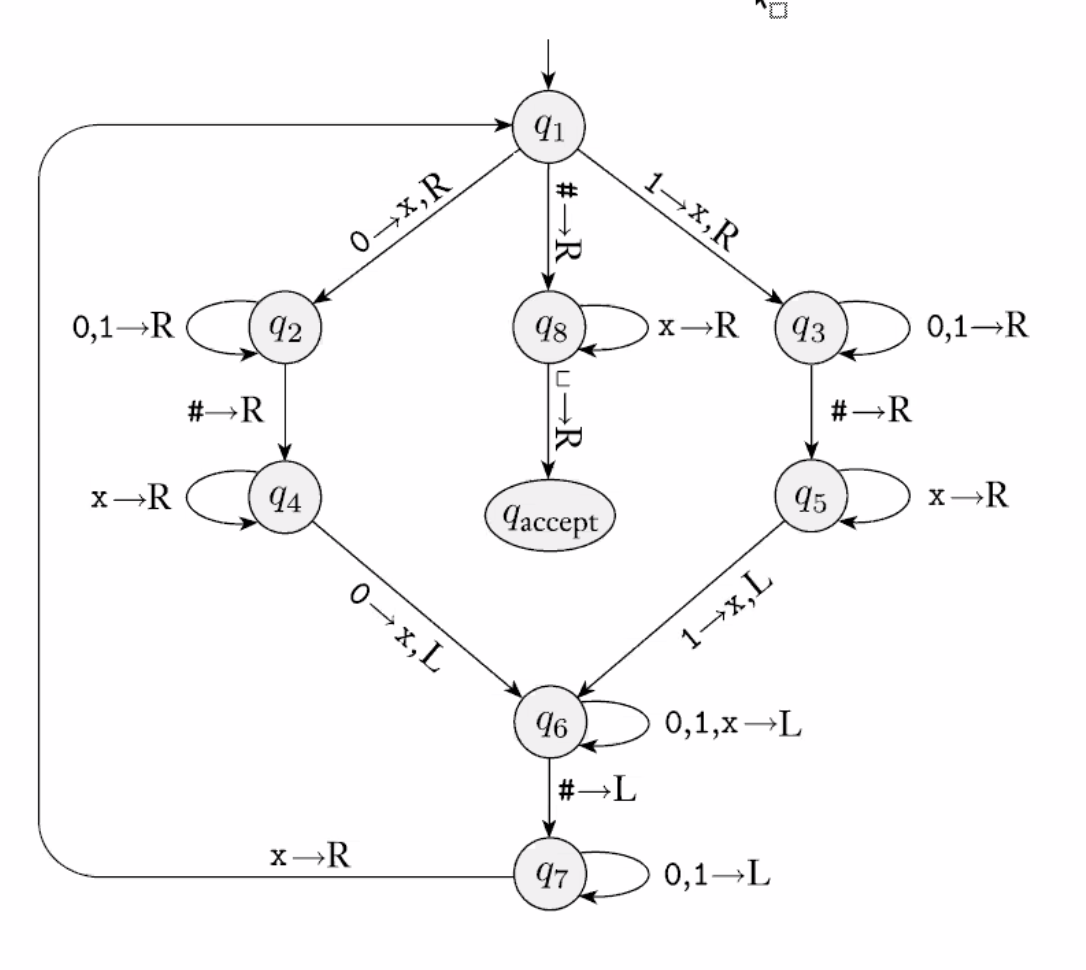
Ex 8¶
ww - without the boundary
\(\Gamma = \{a, b, \dashv, à. á, \text{similar marks for b}\}\)
- Scan L to R, counting symbols mod 2.
- If not even, reject
- When reach end, put down an end marker \(\dashv\)
- Then repeatedly scan left and right over tape
- When scanning R to L mark first unmarked a or b with á
- When scanning L to R mark first unmarked a or b with à
- Continue until all symbols of input are marked (finds middle of string)
- Repeatedly scan L to R
- Remember and erase first à symbol
- Check first á matches and erase
- Reject if no match
- When all symbols erased, reject
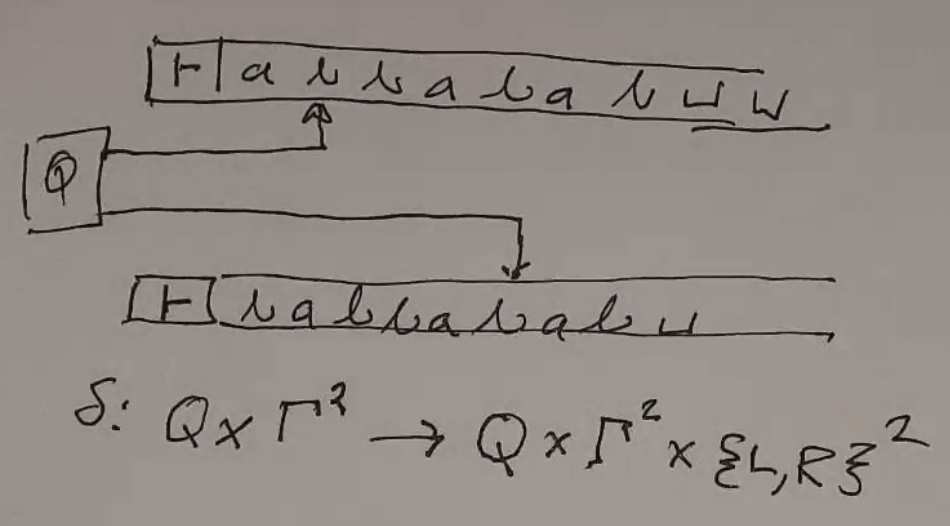
Universal TM¶
Given:
- initial tape information
- the functional matrix for a TM
it is possible to simulate the operation of another TM.
- scan symbol under read/write head
- look up entry in function table for current state and the symbol read
- write second symbol of entry
- move r/w head according to 3rd symbol entry
- set current state to first symbol of entry
- if current state acc or rej do so
- goto 1
Special Coding¶
Need way to distinguish between 3 kinds of symbols: L/R, input/tape alphabet, states

Maybe we can use binary:

Halting Problem¶
For any universal machine U, it acts the same way on a string as the machine it simulates. Is it possible to make a universal machine that halts and rejects if the simulated machine loops?

No. No it is not. Use diagonalization:
Diagonalization Review¶
The real numbers are not countable.
- Assume R is countable
- So it is possible to write a list of R
- Consider a list of numbers (in this example, binary decimals):
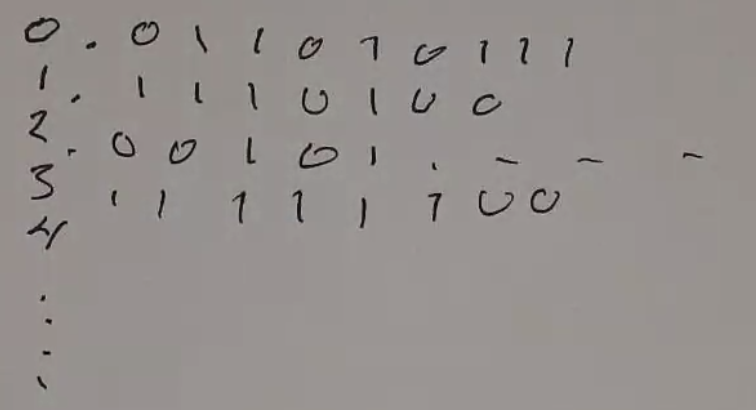
- Given this, it is possible to define a real number that is not in the list:
- the first digit is the opposite of the first position of the first number in the list
- the second digit is the opposite of the second position of the second number
- etc
- so the number must be different from all other numbers in the list
- which means it must not be able to make a list, so R cannot be countable.
Proof¶
- let x be a binary number
- let \(M_x\) be the TM with the encoding x
- if x is not a valid TM encoding, \(M_x\) halts
- consider the matrix, encoding whether each machine halts on a given input:
+-------+---+---+---+----+----+-----+----+-----+
| | e | 0 | 1 | 00 | 01 | 10 | 11 | ... |
+=======+===+===+===+====+====+=====+====+=====+
| M_e | H | H | H | H | H | H | H | |
+-------+---+---+---+----+----+-----+----+-----+
| M_0 | | | | | | | | |
+-------+---+---+---+----+----+-----+----+-----+
| M_1 | | | | | | | | |
+-------+---+---+---+----+----+-----+----+-----+
| M_00 | | | | | | | | |
+-------+---+---+---+----+----+-----+----+-----+
| M_01 | | | | | | | | |
+-------+---+---+---+----+----+-----+----+-----+
| ... | | | | | | | | |
+-------+---+---+---+----+----+-----+----+-----+
| M_... | H | L | H | L | L | ... | | |
+-------+---+---+---+----+----+-----+----+-----+
- Assume K exists that can determine, if given some machine M and string x, whether M halts on x
- Build N using K
- On input x:
- N applies K to \(M_x, x\)
- run K on \(M_x x\)
- if K accepts (i.e. \(M_x\) halts), N loops
- if K rejects, N accepts
- (note: this is the diagonalization argument on the matrix above)
- So N is different on at least one given string for every \(M_x\) in the table above
- So we have constructed an impossible machine, since it is not in the list of all possible machines above, so K cannot exist
Example¶
m = 999
while m > 1:
if m % 2 == 0:
m = m // 2
else:
m = 3 * m + 1
Is there any value of m such that this loop never halts? We don’t know!
Reduction¶
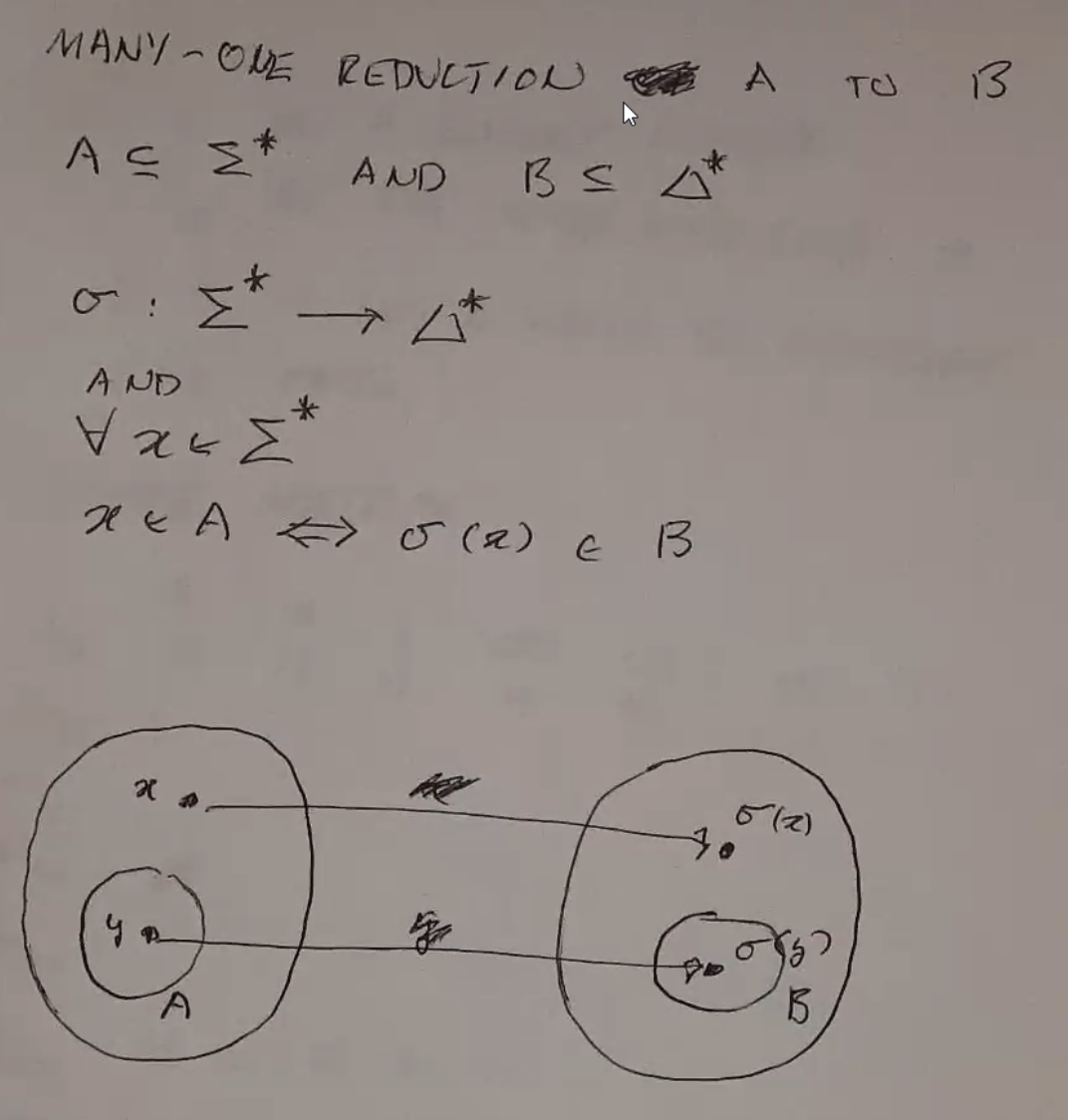
Ex. Halting Problem v. Membership Problem

- Left side: reducing the halting problem to the membership problem
- Right side: reducing the membership problem to the halting problem
You can use this to show that the membership problem is not solvable.
Rice’s Theorem¶

For each of these, there is an algorithm that can solve these problems for finite automata:

However, these are not solvable for Turing Machines.
Definitions¶
- Recursively Enumerable: if \(S = L(M)\) for some TM (i.e. TM doesn’t loop)
- Decidable: a property is decidable if the set of strings with property is recursive
- i.e. a total TM accepts strings with prop and rejects without prop
How do we find the set of all strings a TM accepts?

Thm¶
Any non-trivial property of a recursively enumerable set is undecidable.
Proof¶
- Let p be a non-trivial property of a recursively enumerable set such that:
- \(P(A)\) = T or F
- \(P(\emptyset)\) = F
- p is non-trivial \(\implies \exists A\) a recursively enumerable set that has p
- let K be a TM that accepts A
- Let M and M’ be defined as such:
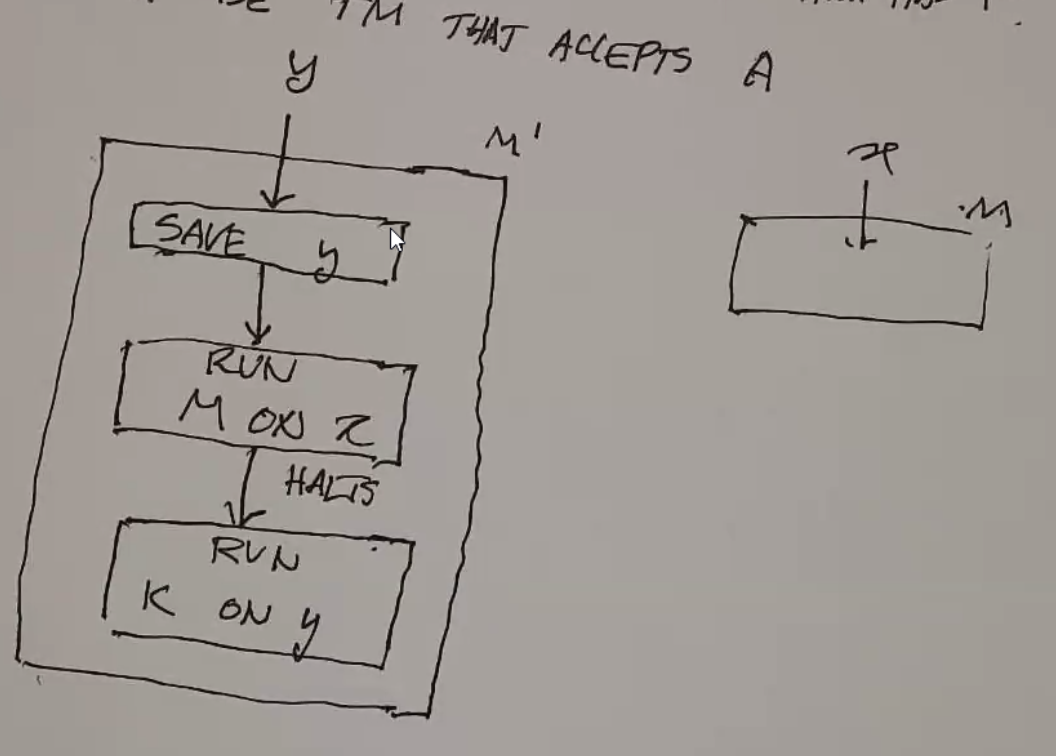
- above: M halts on x \(\implies L(M') = A\)
- M does not halt on x \(\implies L(M') = \emptyset\)
- \(L(M') = A \implies P(L(M')) = P(A) = T\)
- \(L(M') = \emptyset \implies P(L(M')) = P(\emptyset) = F\)
- Reversing this, if we can decide the property, then we can tell if M halts on x.
- The halting problem is not solvable, so this problem is not solvable.
Conclusion¶
\(\text{regular languages} \subset \text{CFLs} \subset \text{recursive} \subset \text{RE} \subset \Sigma^*\)
There are a lot of languages that are not expressible by a TM! There are infinite subsets of \(\Sigma^*\)!