NFA¶
\(N = (Q, \Sigma, \delta, s, F)\), where:
- \(Q\) is a finite set of states
- \(\Sigma\) is a finite set of symbols (input alphabet)
- \(\delta: Q \times \Sigma \to P(Q)\) is the transition function
- the transition function relation on \((Q \times \Sigma) \times Q\)
- \(\delta(p, a) \in P(Q)\)
- the set of all states N can move to from p in one step under the symbol a
- \(p \to^a q\) in \(q \in \delta(p, a)\)
- \(\delta(p, a)\) can be empty set
- \(s \in Q\) is the start state
- \(F \subseteq Q\) are the accept/final states
Extended Transition Function
- \(\delta^*(q, \epsilon) = \{q\}\)
- \(\delta^*(q, a) = \delta(q, a)\)
- \(\delta^*(q, xa) = \bigcup_{p \in \delta^*(q, x)} \delta(q, a)\)
Accept
\(w \in \Sigma^*\) is accepted if \(\delta^*(s, w) \cap F \neq \emptyset\)
(a string will be accepted if it’s possible to accept the string)
Note
It is trivial to prove that every DFA is also a NFA (if the output if the DFA transition is put into a set).
Examples¶
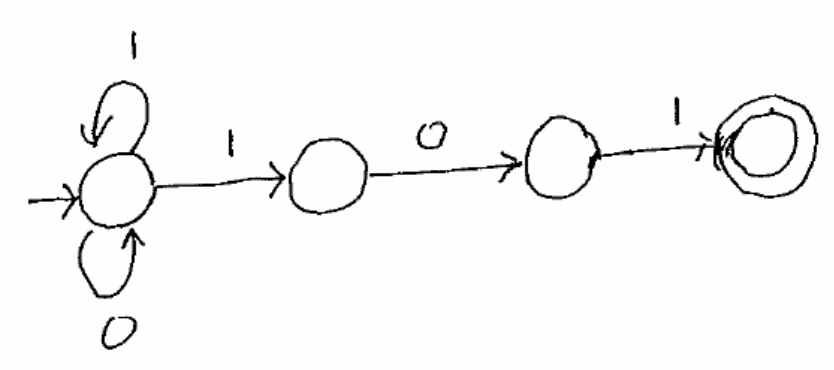
String ends with 101.
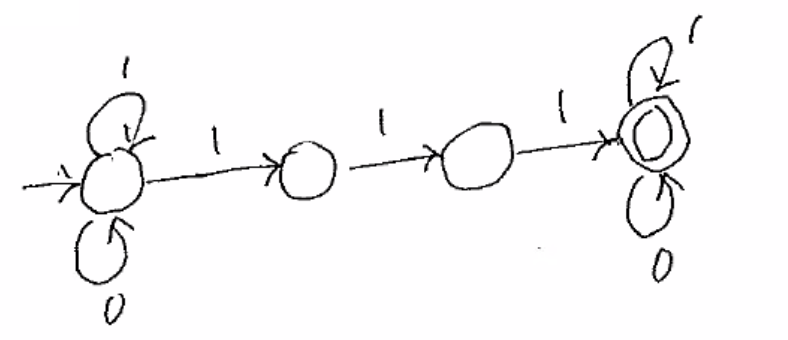
String contains 111.
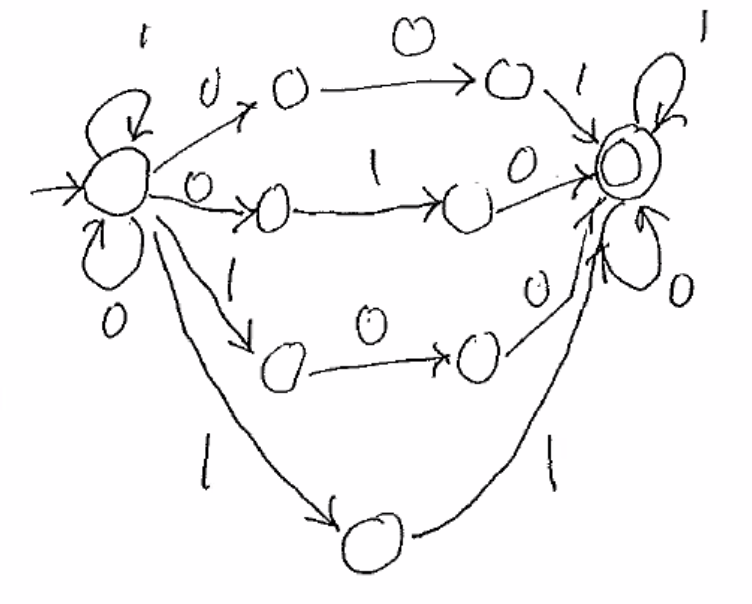
String contains 001 or 010 or 100 or 11.
NFAs are easier to design.
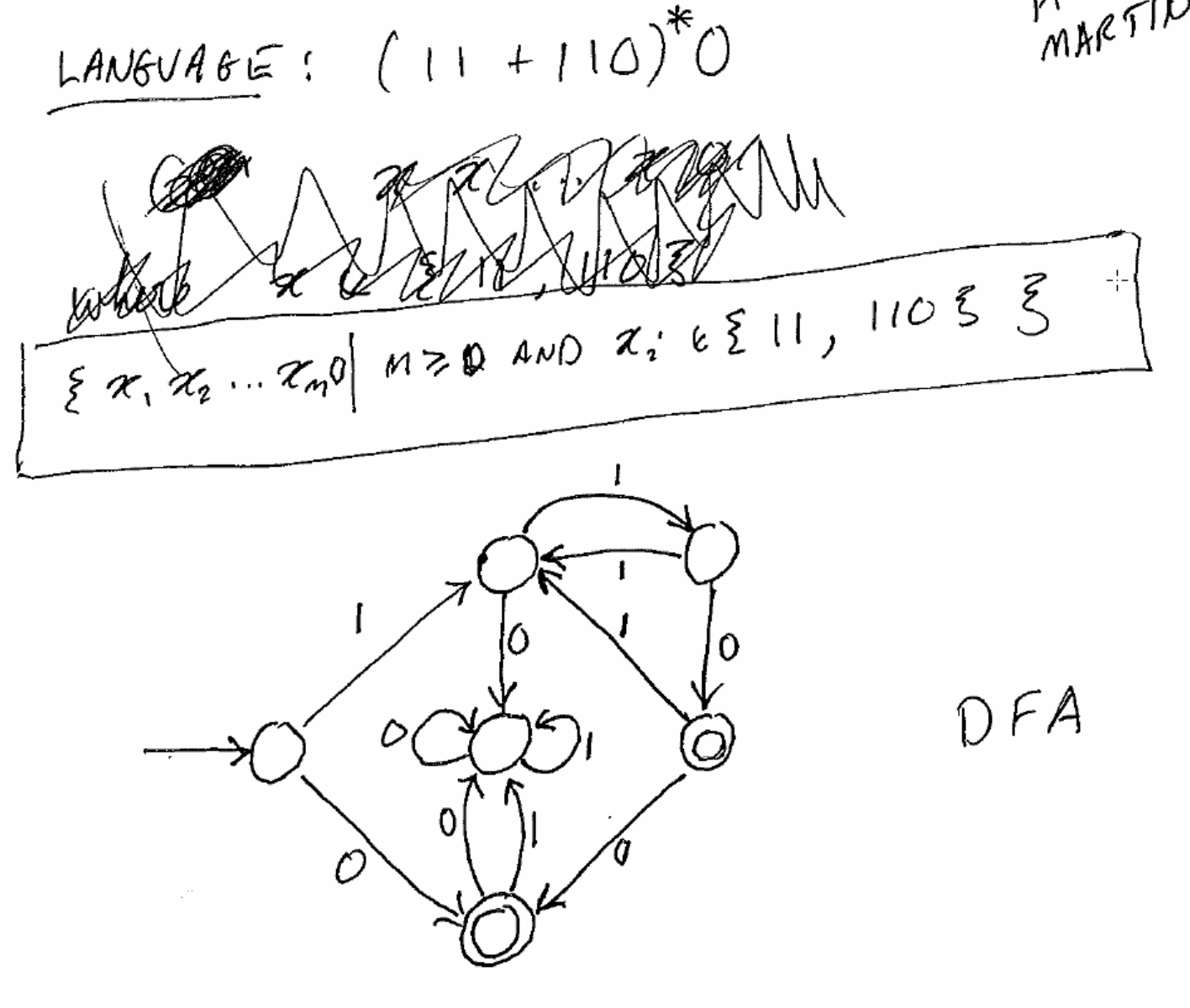
as an NFA:
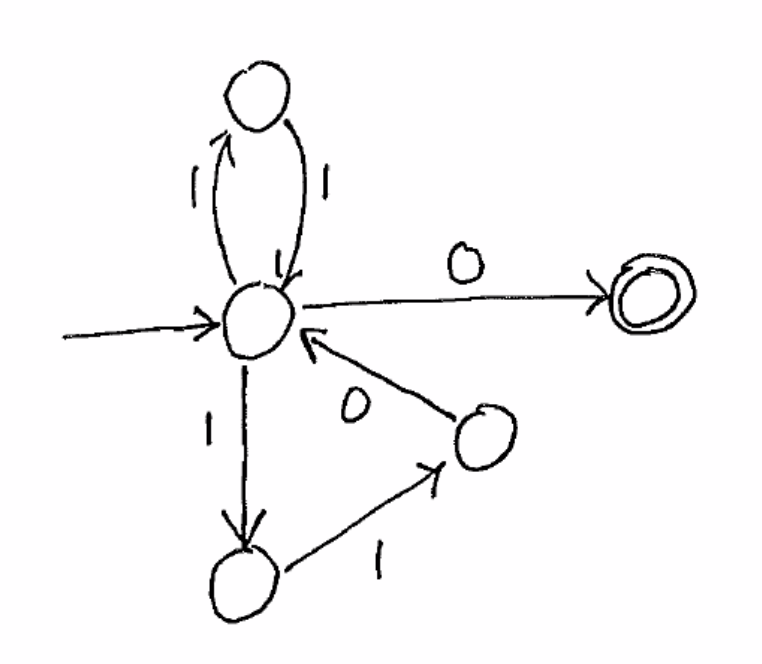
And a weird one:
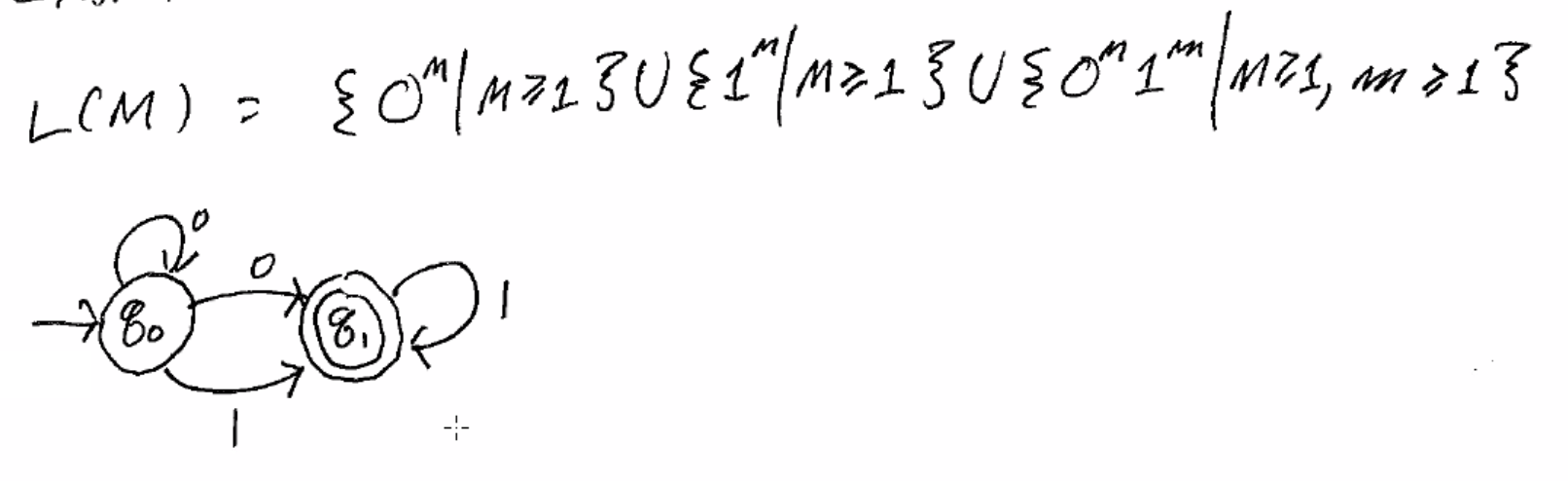
or
Subset Construction¶
aka the Rabin-Scott theorem
Given a NFA \(N = (Q_N, \Sigma, \delta_N, s_n, F_n)\), it is possible to construct a DFA:
\(M = (Q_D, \Sigma, \delta_D, s_D, F_D)\)
- \(Q_D = P(Q_N)\)
- \(s_D = \{s_N\}\)
- \(F_D = \{P \subseteq Q_N | P \cap F_N \neq \emptyset\}\)
- \(\delta_D: Q_D \times \Sigma \to Q_D\) (i.e. \(P(Q_N) \times \Sigma \to P(Q_N)\))
- \(\delta_D(P, a) = \bigcup_{p \in P} \delta_N(p, a)\) for \(P \subseteq Q_N\)
TLDR: the states of the DFA are the sets of states possible at any given point in the NFA.
Ex.
Given this language and NFA:
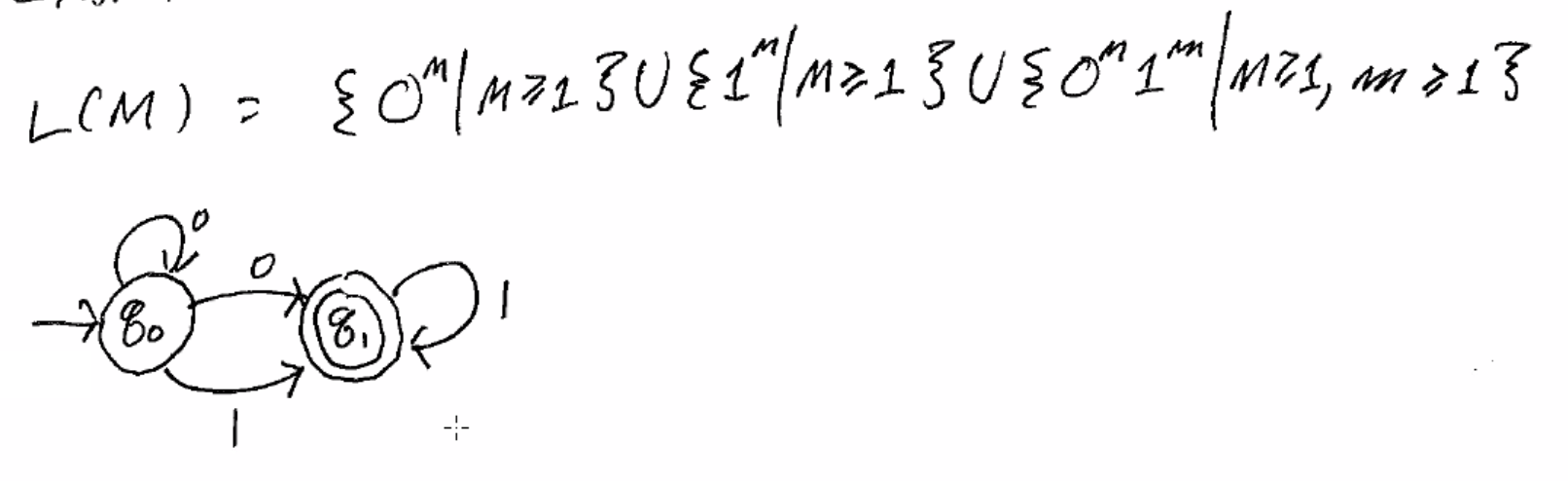
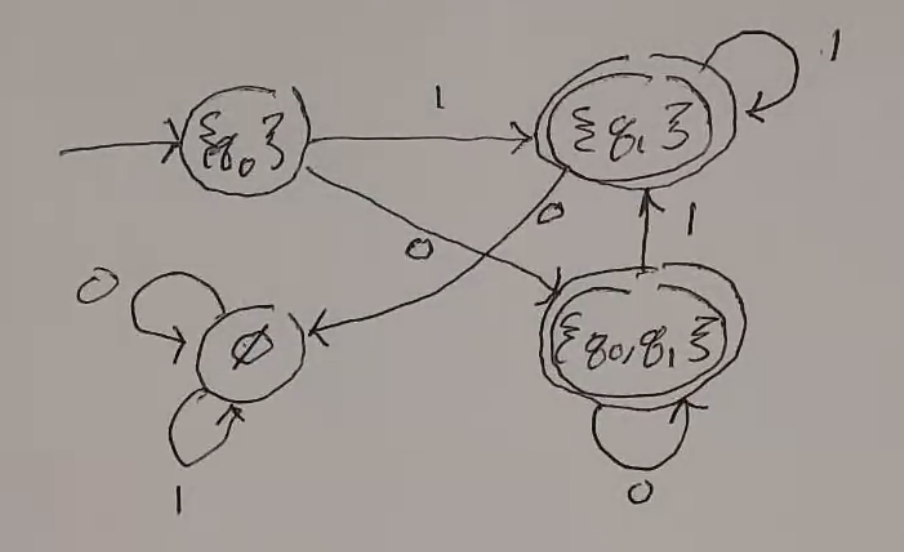
the DFA looks like:
Ex 2.
A language of 0s and 1s, where the second-last symbol is a 0.
NFA:
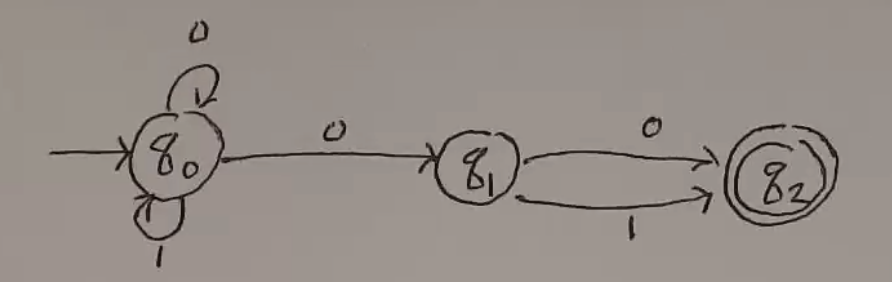
DFA:
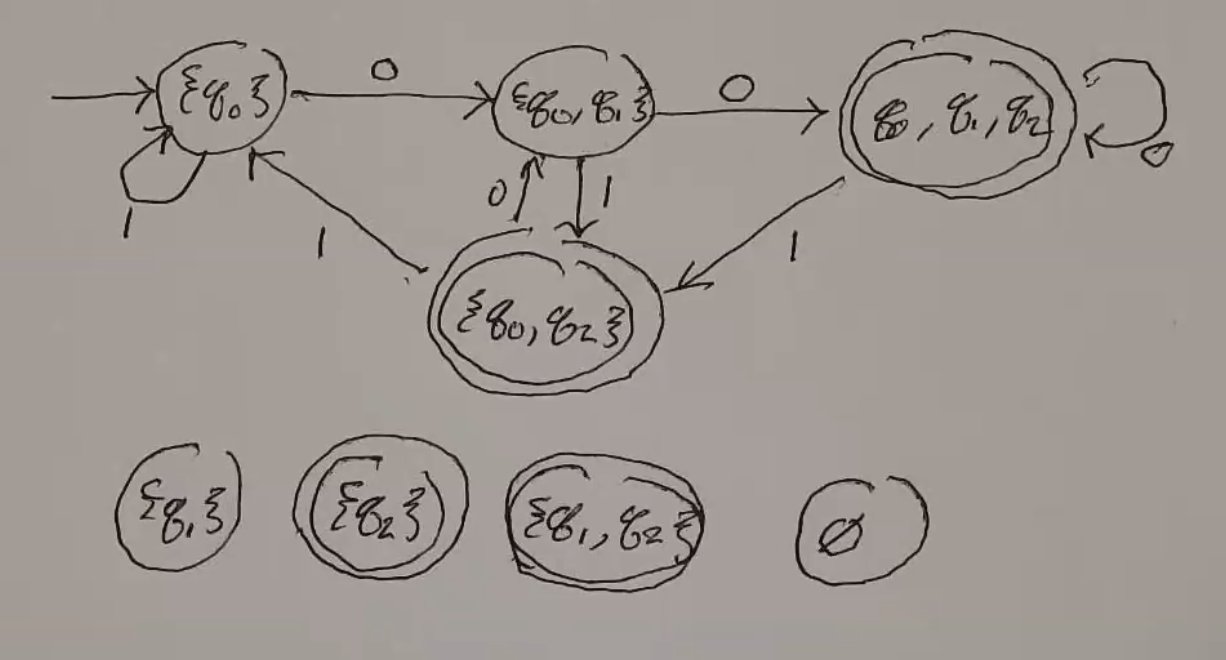
Ex 3.
The family of languages \(L_n = \{w \in \{0, 1\}^* | \text{ the nth position from end is 1}\}\)
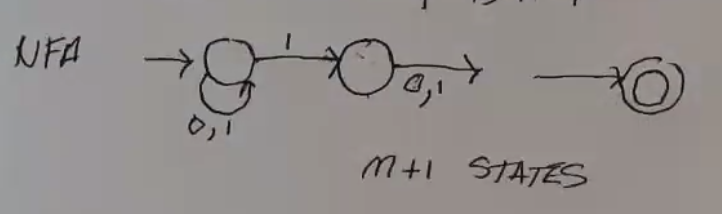
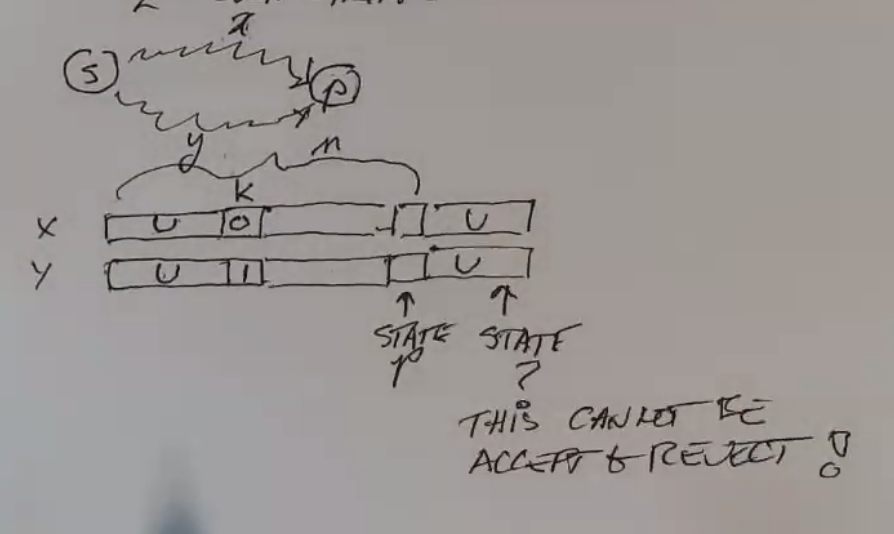
The DFA for \(L_n\) cannot have less than \(2^n\) states. Pf:
- Assume there is some DFA that recognizes \(L_n\) that has less than \(2^n\) states.
- Consider strings of length n. There are \(2^n\) such strings.
- Consider two arbitrary strings x and y that both end in a state p.
- Consider the first position those two strings differ k.
- Call the same identical part of the string u.
- If we redefine x and y such that k is the start and u is moved to the end, we get two strings with different characters n from the end, only one of which is accepted
- Contradiction!
Epsilon Moves¶
Epsilon moves allow us to jump to another state without taking any input.
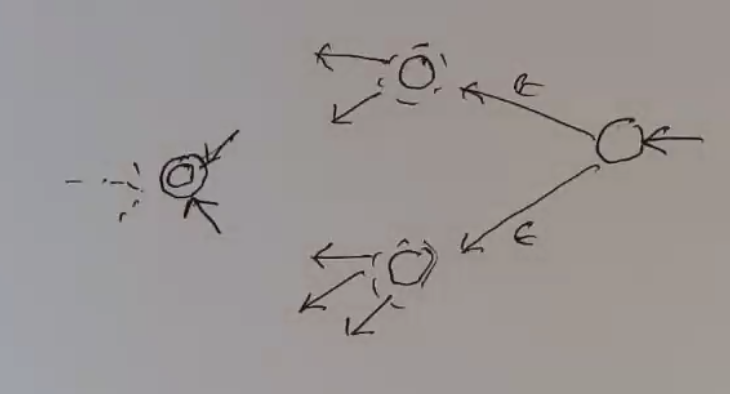
Consider \(L = \{1^n | n \text{ is a multiple of 3 or 5}\}\)
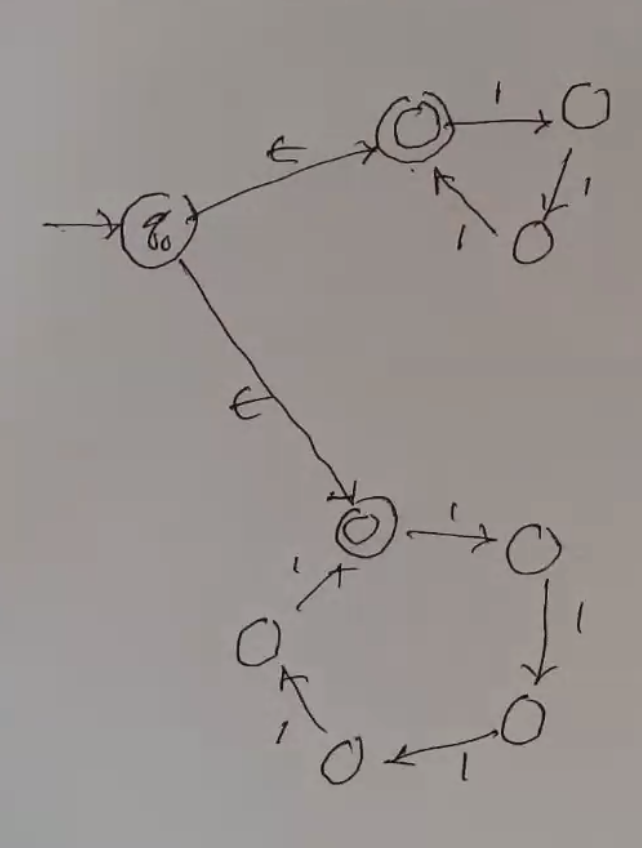
While epsilon moves make NFAs easier to design, any NFA with epsilon moves can be rewritten as one without.
Formally:
\(M = (Q, \Sigma, \delta, s, F)\), where:
- \(\delta: Q \times (\Sigma \cup \{\epsilon\}) \to P(Q)\) is the transition function
- \(\delta(q, \epsilon) \to P \subseteq P(Q)\) does not move the scan head
Thm:
For every \(\epsilon\)-NFA there is an NFA \(\hat{M}\) s.t. \(L(M) = L(\hat{M})\).
- \(\hat{M} = (\hat{Q}, \Sigma, \hat{\delta}, \hat{s}, \hat{F})\), where:
- \(\hat{Q} = Q\)
- \(\hat{s} = s\)
- \(\hat{\delta}: \hat{Q} \times \Sigma \to P(\hat{Q})\)
- \(\hat{\delta}(p, a) = \{q | \text{ there are states } p_1, p_2 \text{ s.t.:}\)
- \(p_1 \in E(p)\)
- \(p_2 \in \delta(p_1, a)\)
- \(q \in E(p_2) \}\)
- where \(E(p)\) is the set of all states reachable from p using only epsilon moves.
- new accept states are states that can reach accept states with epsilon moves
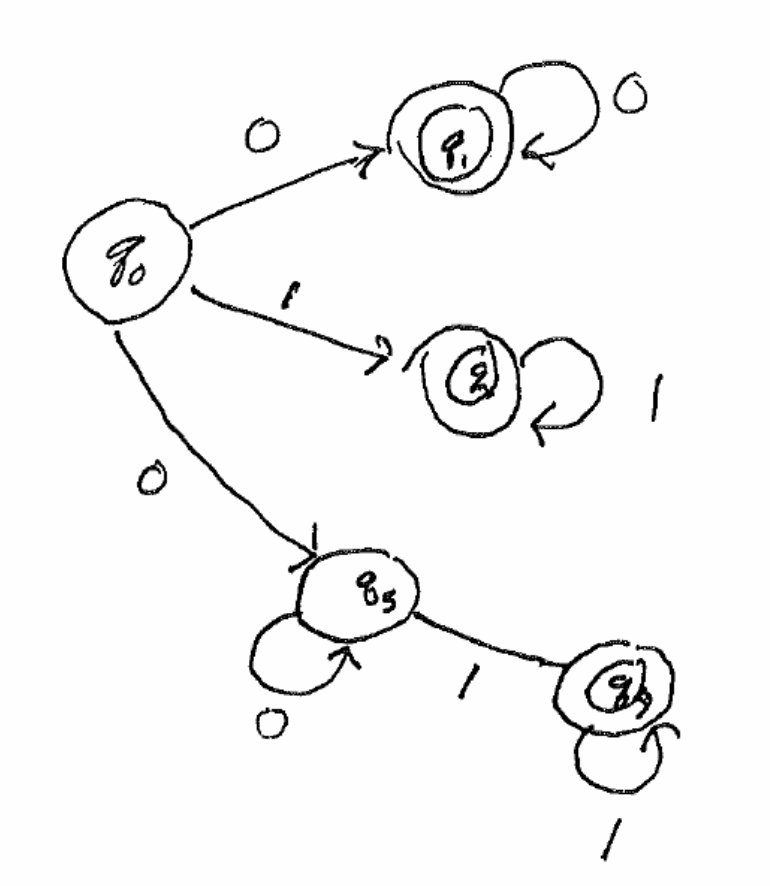
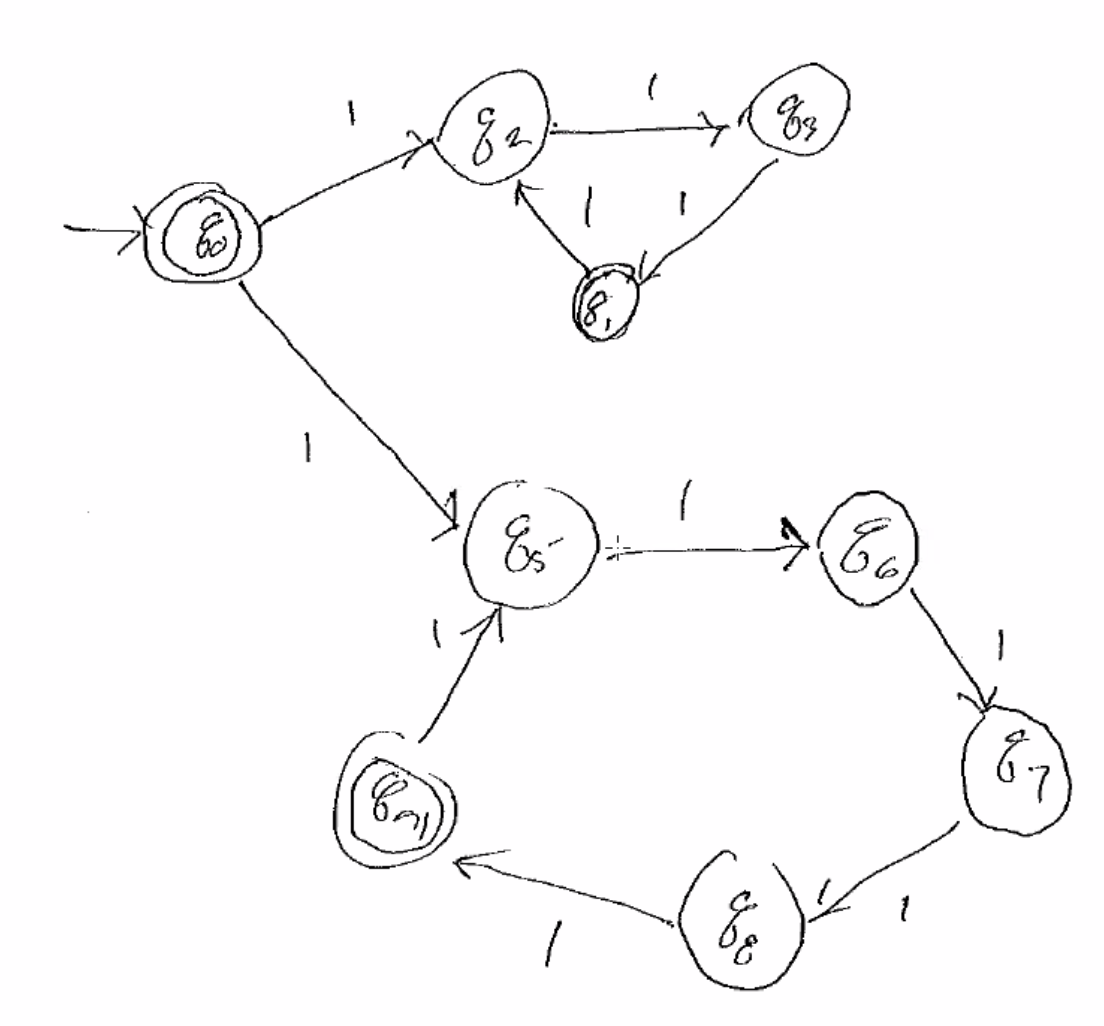
Ex:
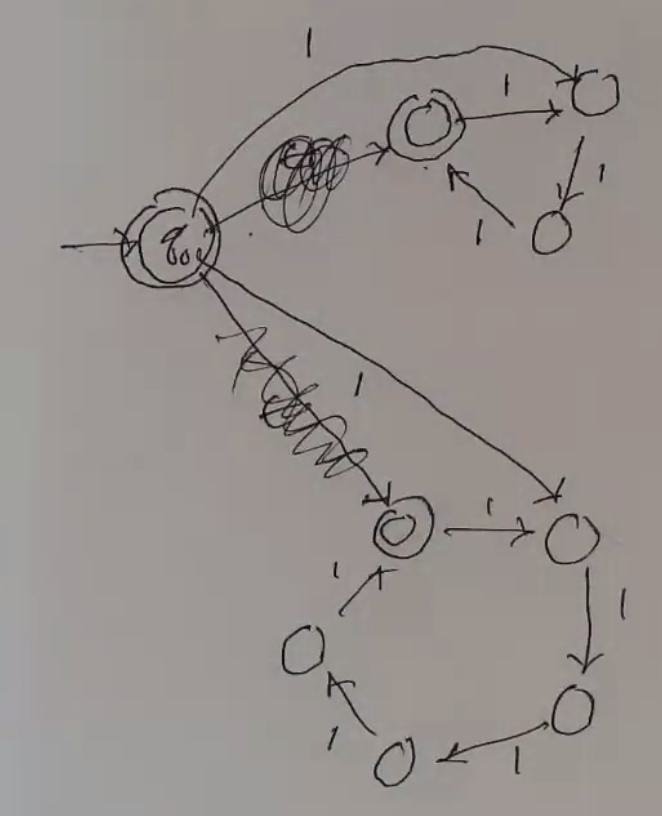
(cleaner view)
Closure¶
Regular languages are closed under:
- complement
- union
- intersection
- difference
- concatenation
- kleene star
- quotient
- reversal
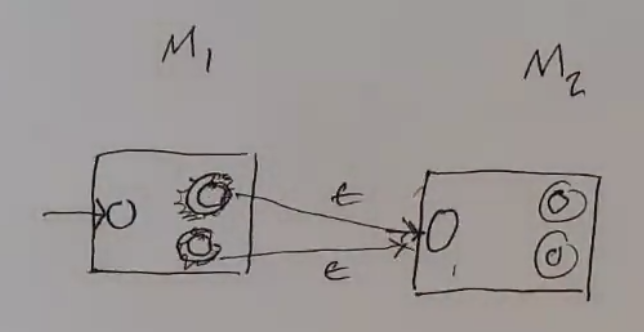
Concatenation¶
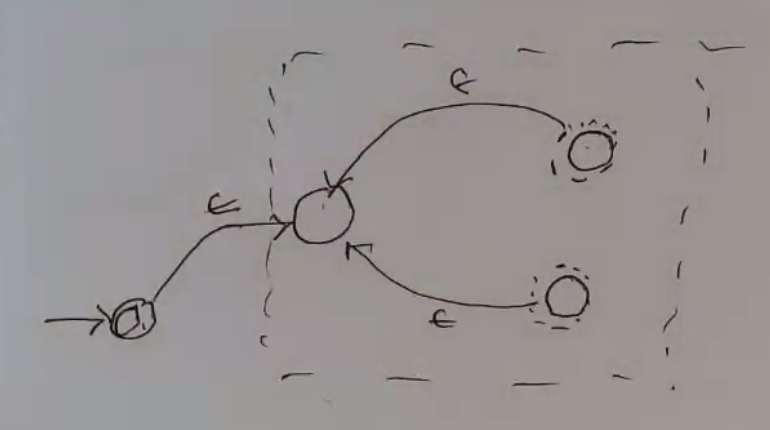
Kleene Star¶
The set of all strings that can be generated by concatenating 0 or more strings in a set of strings.
Reversal¶
Reverse all arrows, make start state accept state, make accept states the start states (using epsilon).