Push-Down Automata¶
PDAs give us a form of memory by introducing a stack, which has infinite space but containing a finite number of elements:

Formal Definition¶
\(M = (Q, \Sigma, \Gamma, \delta, s, F)\) where
- \(Q\) is a finite set of states
- \(\Sigma\) is a finite set (symbols - input alphabet)
- \(\Gamma\) is a finite set (symbols - stack alphabet)
- \(\delta: (Q \times (\Sigma \cup \{ \epsilon \}) \times (\Gamma \cup \{ \epsilon \})) \to P(Q \times (\Gamma \cup \{ \epsilon \}))\)
- Takes a state, maybe something from the input, maybe something from the stack (popped)
- Produces some subset of states (non-deterministic) and something to push on stack, optionally
- \(s \in Q\) is the start state
- \(F \subset Q\) is the accept states
Ex 1¶
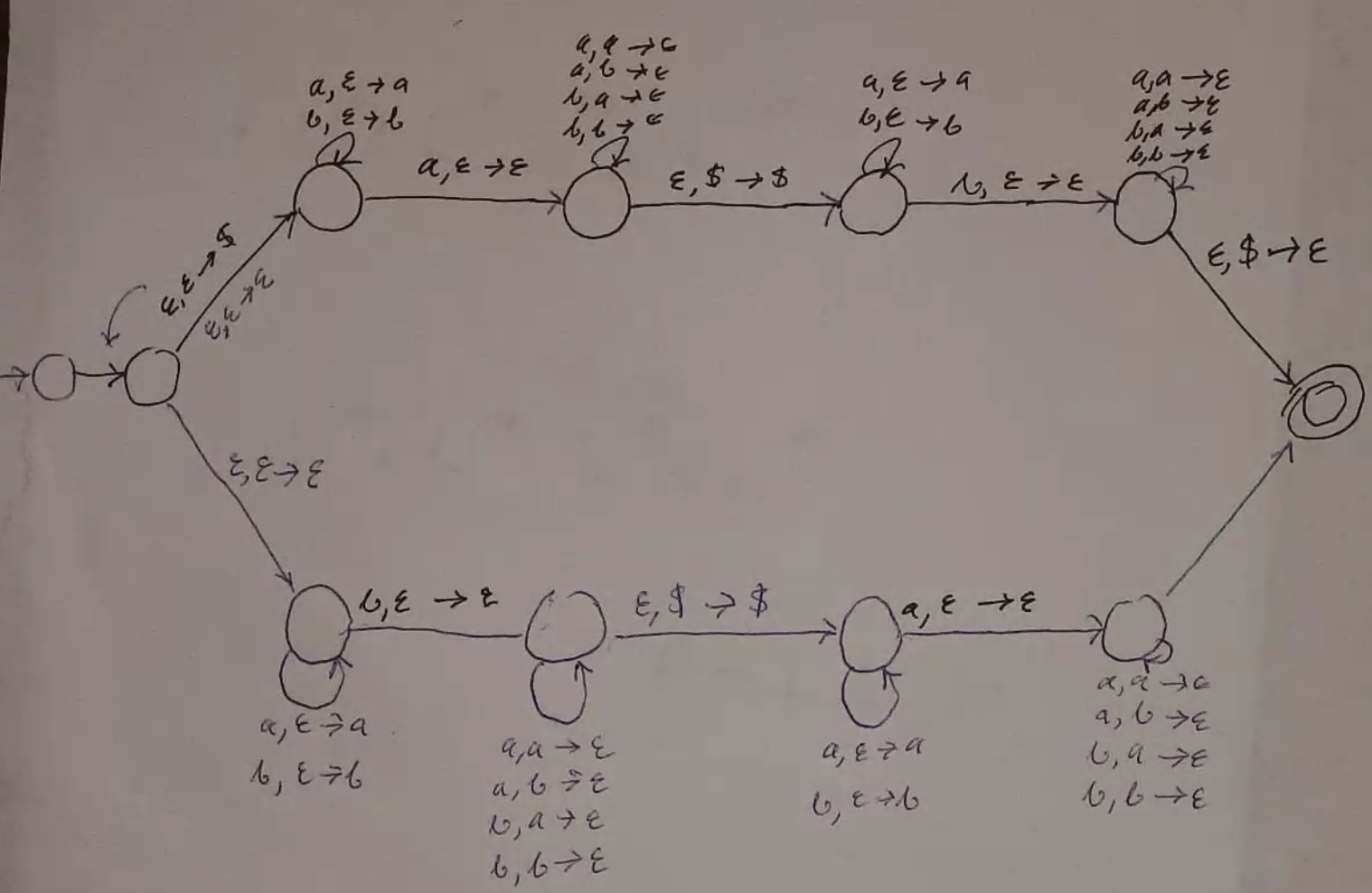
- \(L = \{ 0^n 1^n | n \geq 0 \}\)
- \(Q = \{q_1, q_2, q_3, q_4\}\)
- \(\Sigma = \{0, 1\}\)
- \(\Gamma = \{ \hat{0}, $ \}\)
- \(s = q_1\)
- \(F = \{ q_1, q_4 \}\)
- \(\delta\) is represented by this state diagram:
- Design: Push 0s onto the stack, pop an equal number of 1s.

\(x, y \to z\) represents whether to read, what to pop, and what to push, if any.

Ex 2¶
\(L = \{ w w^R | w \in \{0, 1\}^* \}\)
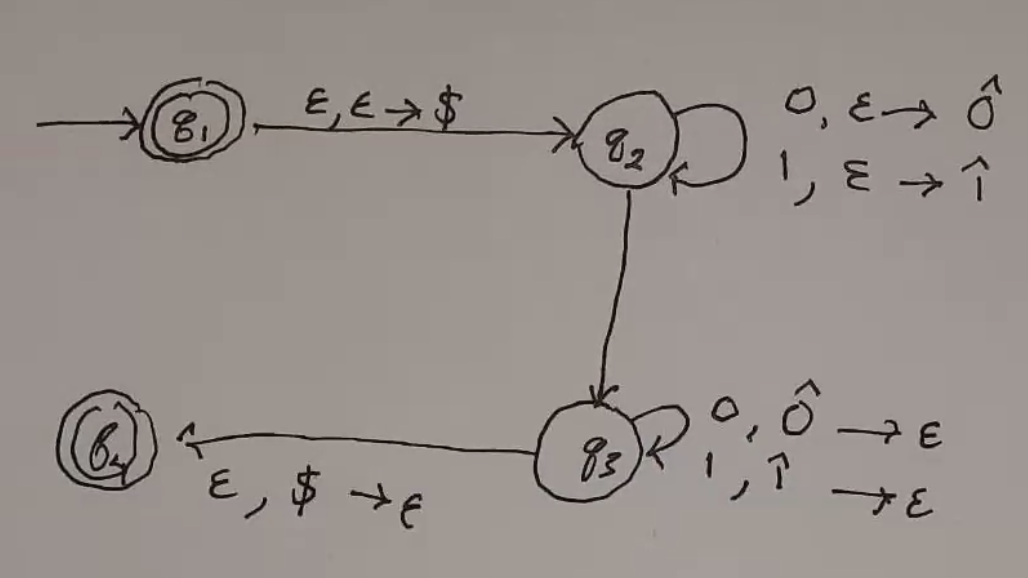
Note
The transition \(q_2 \to q_3\) is nondeterministic and can be an epsilon move.
CFGs¶
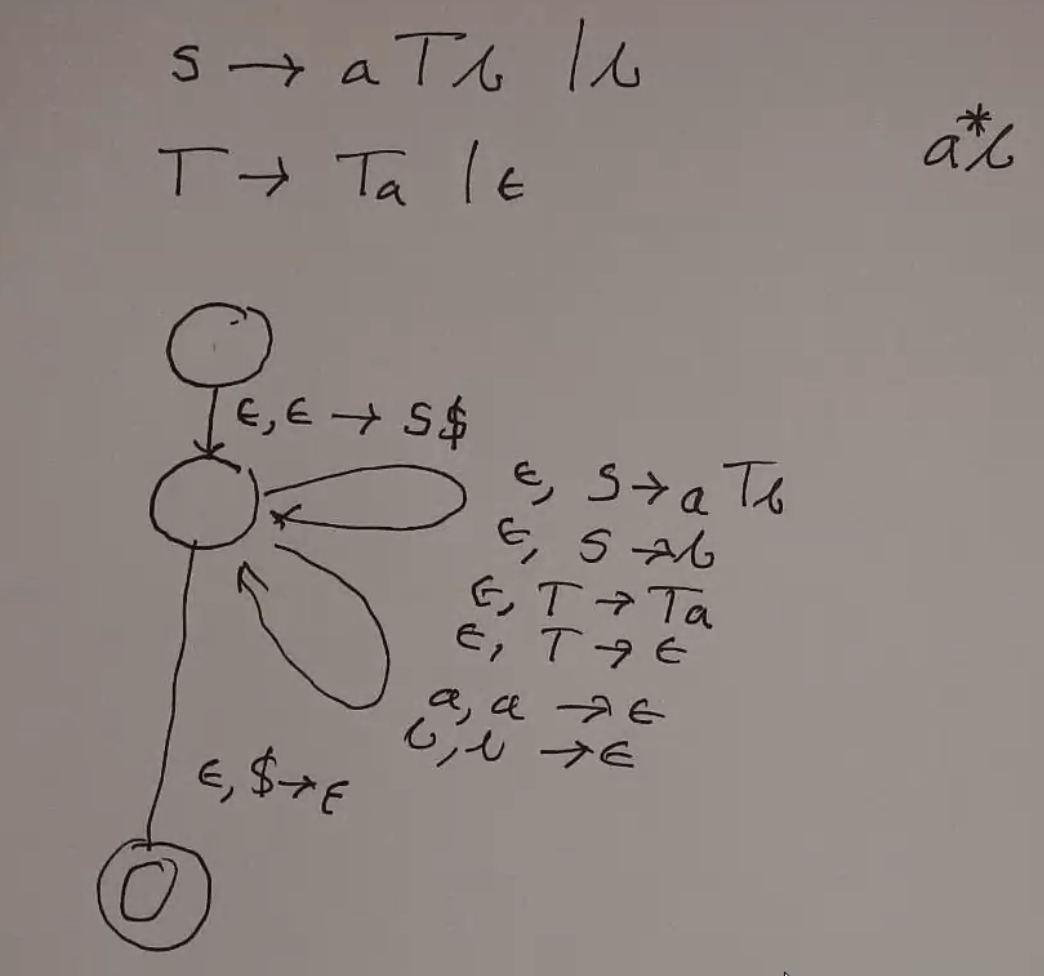
You can make a PDA for any CFG using 3 states:
Place $ and start in stack
Do repeatedly:
If var on top:
Pop it and push right side of rule (*)
If terminal on top:
If it matches the stack, advance read head
If not, fail
If $ on top:
Accept
Note
*: This means we allow pushing entire strings onto the stack. This can be done character-wise, but it’s
faster this way.
Ex 1¶
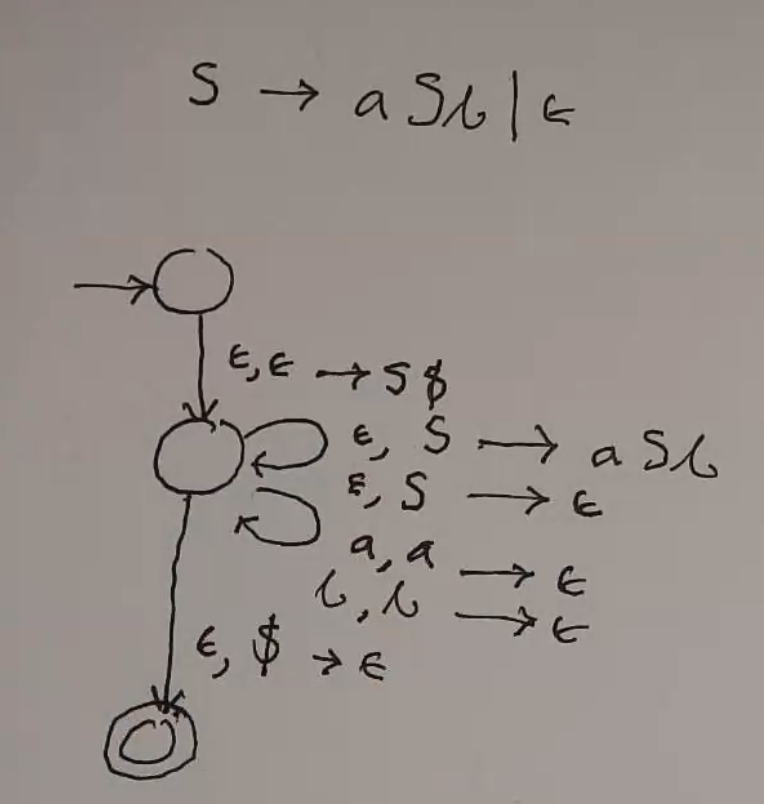
Ex 2¶
CKY Algorithm¶
Given a CFG, how do you determine whether \(x \in L(G)\)?
Examine the substrings (grammar should be in CNF):
Ex 1¶
S := AB | BA | SS | AC | BD
A := a
B := b
C := SB
D := SA
Is aabbab in the language? The table represents ways to get from top to right.
Fill in the diagonals (longest first):
|a|a|b|b|a|b|
0 1 2 3 4 5 6
+-----+-----+-----+-----+-----+-----+---+
| 0 | | | | | | |
+-----+-----+-----+-----+-----+-----+---+
| {A} | 1 | | | | | |
+-----+-----+-----+-----+-----+-----+---+
| {} | {A} | 2 | | | | |
+-----+-----+-----+-----+-----+-----+---+
| {} | {S} | {B} | 3 | | | |
+-----+-----+-----+-----+-----+-----+---+
| {S} | {C} | {} | {B} | 4 | | |
+-----+-----+-----+-----+-----+-----+---+
| {D} | {S} | {} | {S} | {A} | 5 | |
+-----+-----+-----+-----+-----+-----+---+
| {S} | {C} | {} | {C} | {S} | {B} | 6 |
+-----+-----+-----+-----+-----+-----+---+
Since it is possible to get from 0 to 6 using the start variable, the string is in the language.
Ex 2¶
S := AB | BC
A := BA | a
B := CC | b
C := AB | a
Is baaba in the language?
|b|a|a|b|a|
0 1 2 3 4 5
+-----------+--------+--------+--------+--------+---+
| 0 | b | | | | |
+-----------+--------+--------+--------+--------+---+
| {B} | 1 | a | | | |
+-----------+--------+--------+--------+--------+---+
| {A, S} | {A, C} | 2 | a | | |
+-----------+--------+--------+--------+--------+---+
| {} | {B} | {A, C} | 3 | b | |
+-----------+--------+--------+--------+--------+---+
| {} | {B} | {S, C} | {B} | 4 | a |
+-----------+--------+--------+--------+--------+---+
| {A, S, C} | {S, A} | {B} | {A, S} | {A, C} | 5 |
+-----------+--------+--------+--------+--------+---+
So the string is in the language.