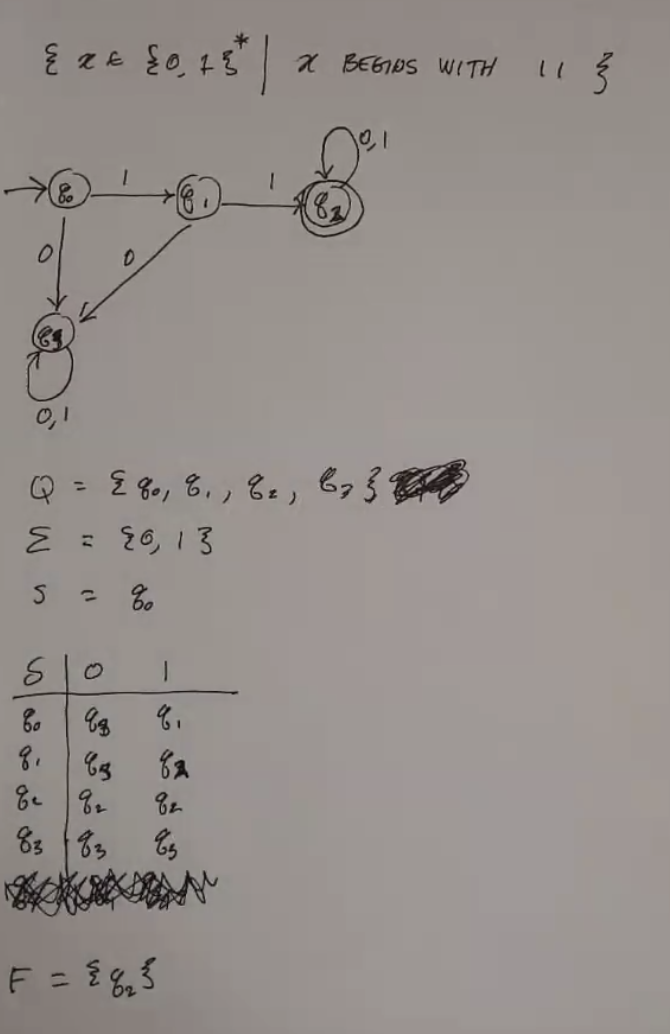
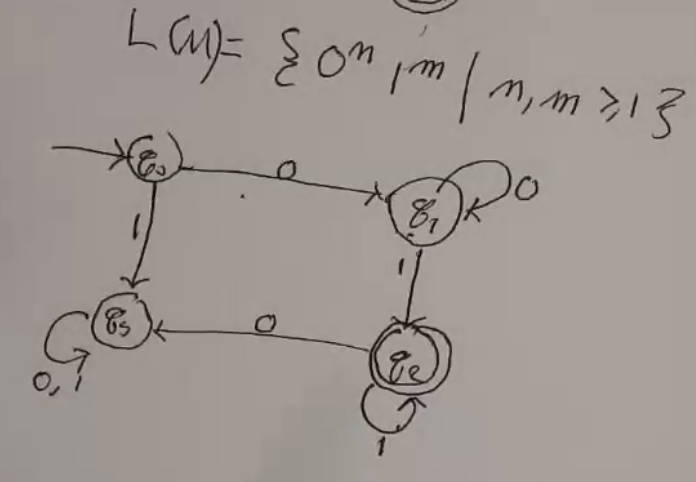
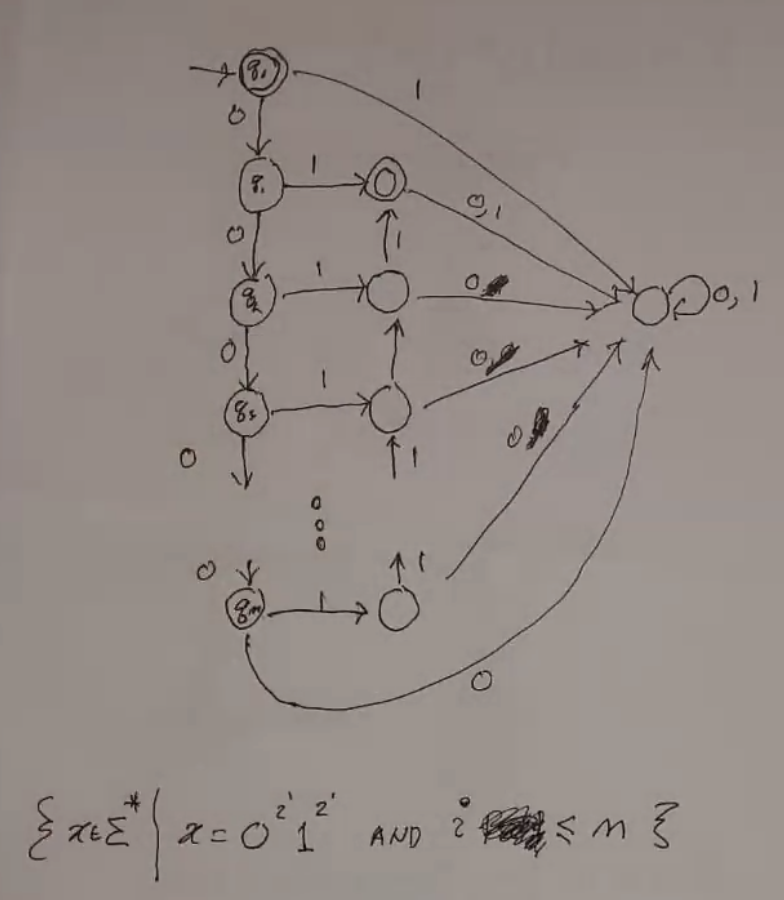
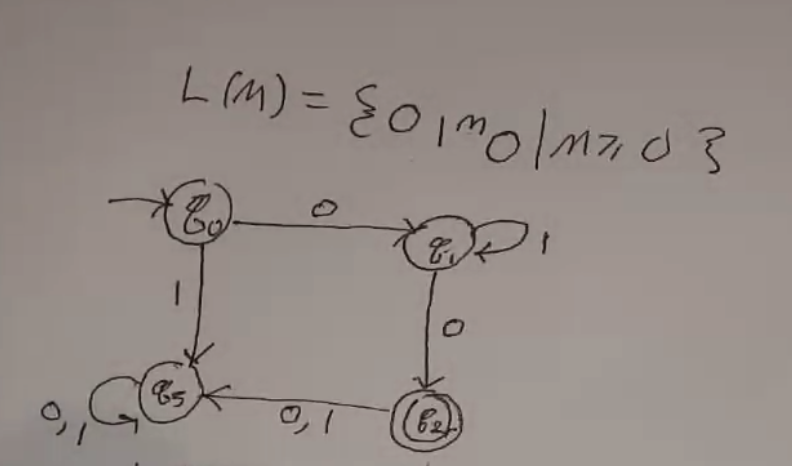DFA

Deterministic Finite Automaton (DFA) is a structure:

\(M = (Q, \Sigma, \delta, s, F)\), where:

• \(Q\) is a finite set of states
• \(\Sigma\) is a finite set of symbols (input alphabet)

• \(\delta: Q \times \Sigma \to Q\) is the transition function

  • given a current state and input, use delta to find the new state

• \(s = q_0 \in Q\) is the start state
• \(F \subseteq Q\) are the accept/final states

Defns:

• \(x \in \Sigma^*\) if accepted by M if M stops in F
• \(L(M)\) is the language of machine M when it consists of all strings the machine accepts
• \(L \subseteq \Sigma^*\) is regular if there is a DFA M s.t. \(L = L(M)\) (some dfa recognizes it)

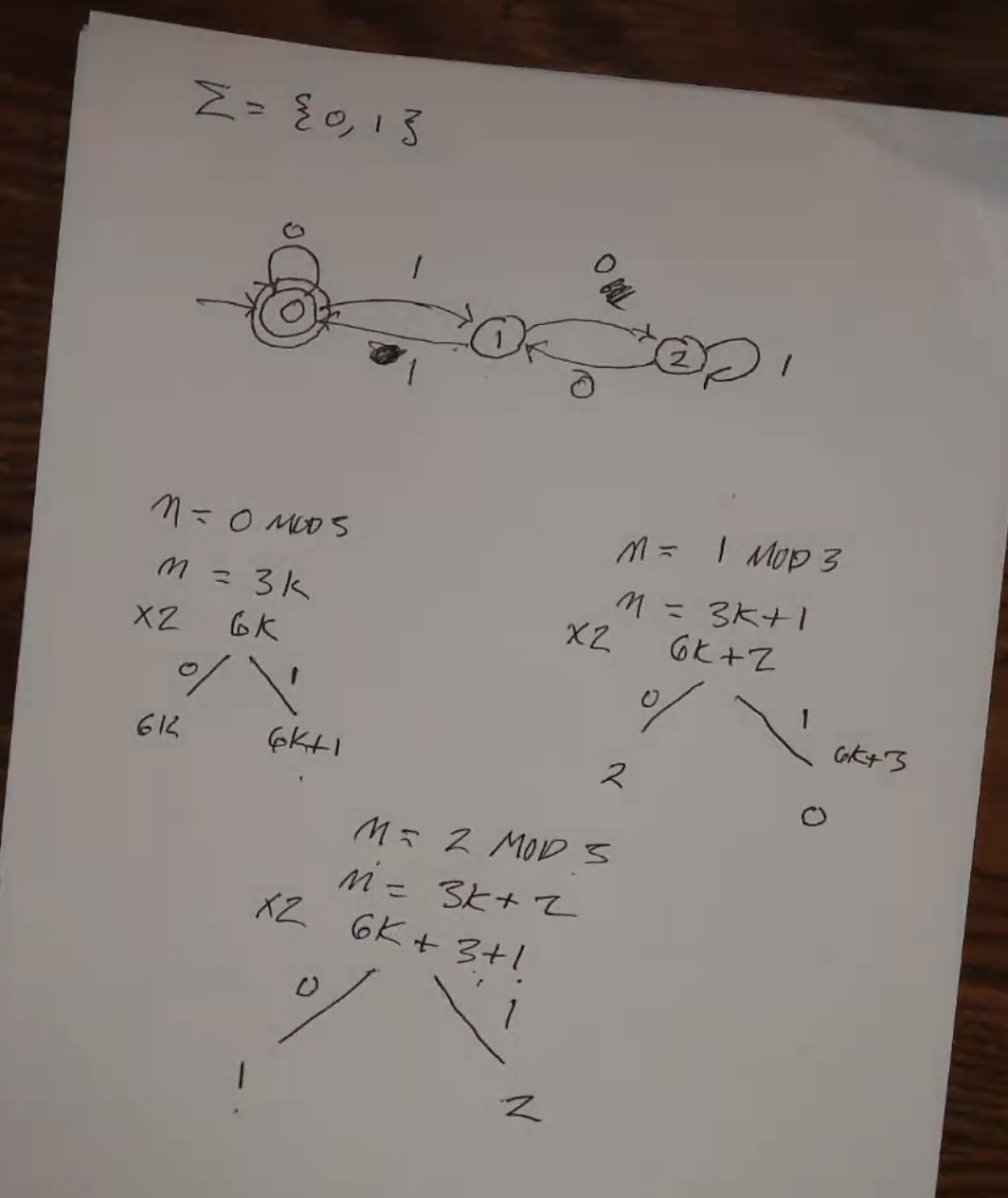
DFAs can be represented using a graph/flowchart thing. Final states are represented by double-bordered nodes.

Note

An example of a non-regular language is \(\{0^m1^m | m \geq 1\}\). (e.g. 01, 0011, 000111, etc)

Note

Any finite language is regular, since it can be represented by just a really huge DFA!

Extended Transition Function

\(\hat{\delta}: Q \times \Sigma^* \to Q\)

Rather than a transition from one state to the next given a symbol, this function maps a starting state and a string to the result after processing what whole string.

Inductice Defn

• For all \(q \in Q, x \in \Sigma^*, a \in \Sigma\):

• \(\hat{\delta}(q, \epsilon) = q\)

  • the extended transition function of any state and the empty string is the same state

• \(\hat{\delta}(q, xa) = \delta(\hat{\delta}(q, x), a)\)

  • just the normal transition plus one more

Thms

• Given a regular language, the complement of that language is also regular. (let the accept states of the DFA be the rejects of the regular language.)

  • \(x \in L(M) \to \hat{\delta}(s, x) \notin F\)
  • \(\hat{\delta}(s, x) \in Q - F = F_c\)
  • \(\hat{\delta}(s, x) \in F_c\)
  • \(x \in L(M_c)\)

Examples

Two Ones

This image shows a DFA that accepts any string starting with two ones.

Even Ones

Consider a DFA that accepts any string with an even number of ones. (\(\Sigma = \{0, 1\}\))

3 As

Consider a DFA that accepts any string that contains at least 3 As. (\(\Sigma = \{a, b\}\))

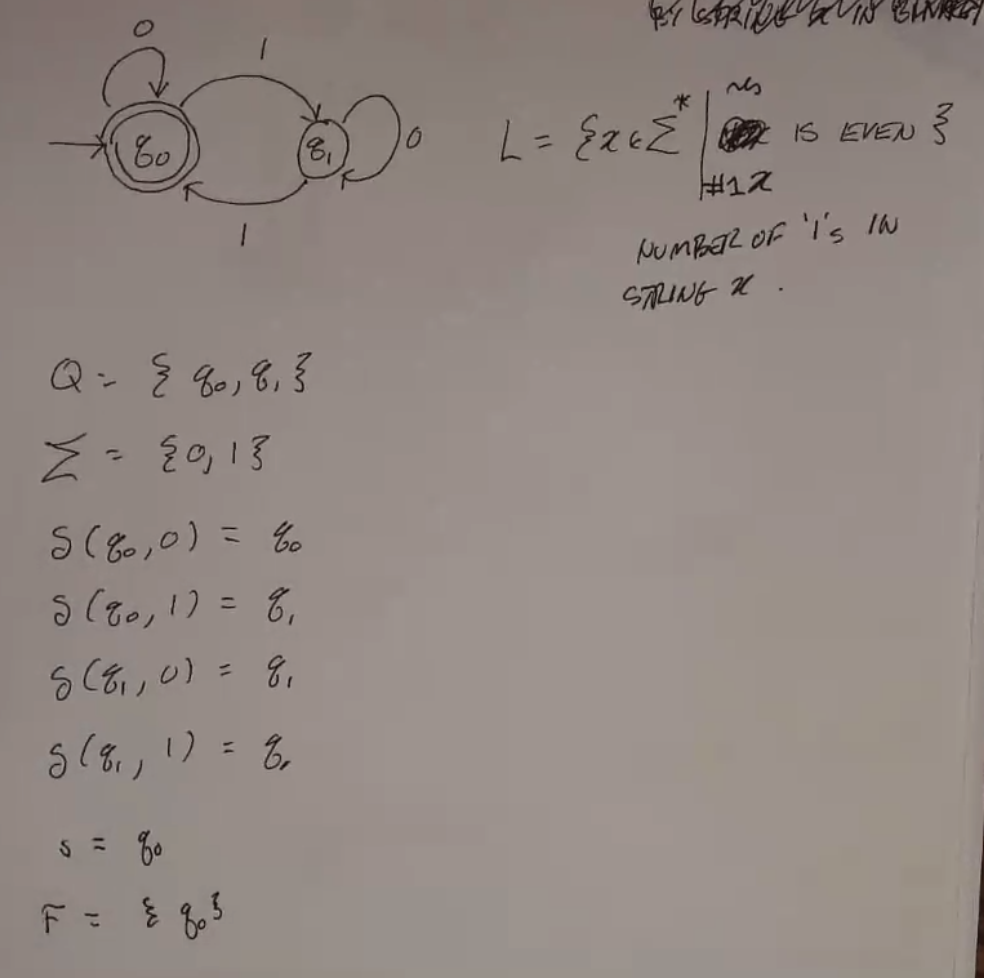
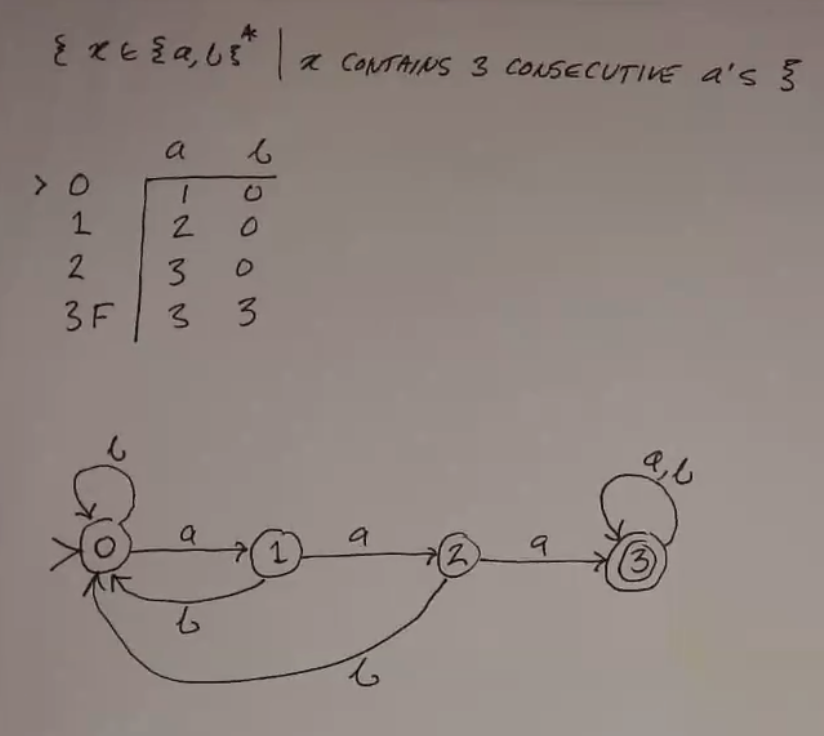
3 Consec As

Consider a DFA that accepts any string that contains at least 3 consecutive As. (\(\Sigma = \{a, b\}\))

0m0

Design a DFA for the language \(L(M) = \{01^n0 | n \geq 0\}\).

00011

Design a DFA for the language \(L(M) = \{0^n1^m | n, m \geq 1\}\).

Note

However, \(L(M) = \{0^n1^n | n \geq 1\}\) does not exist. Such a DFA would have to be infinitely large:

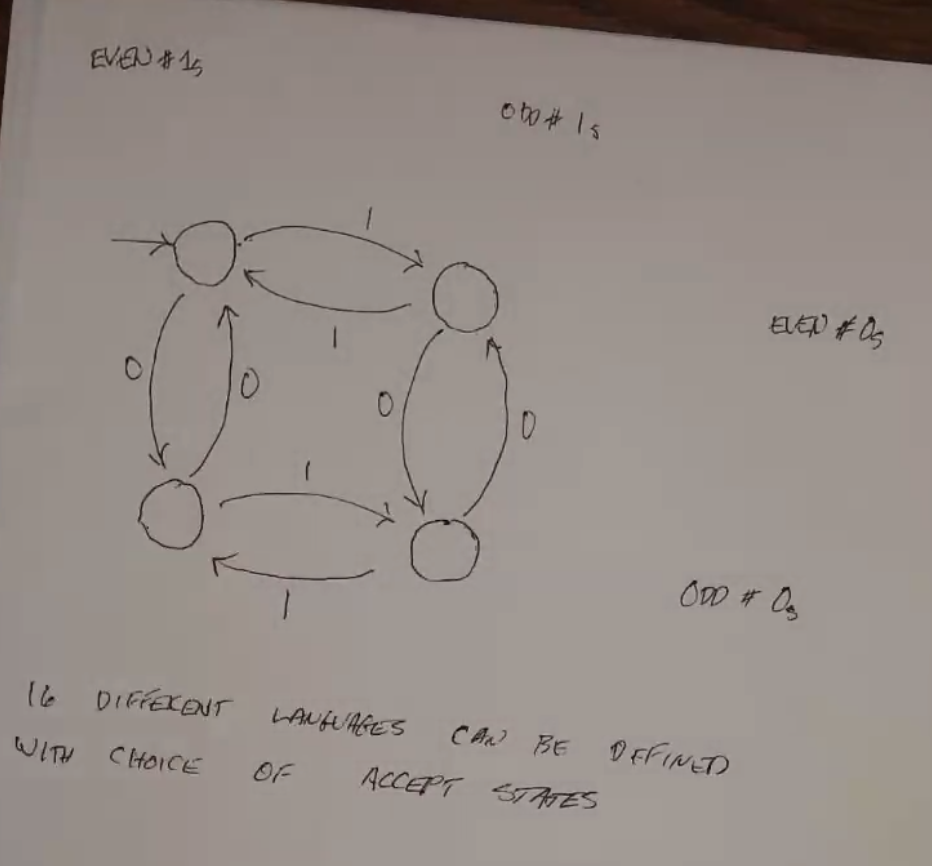
Odds/Evens

This DFA tracks how many 1s and 0s are found in a string. 16 different languages can be defined with choices of accept states:

Div3

Design a DFA for the language of all binary numbers that are divisible by 3

Len3

Strings of length multiple of 3.

Intersection

aka Product Construction

Thm: If languages A and B are regular, then \(A \cap B\) is regular.

• there exists \(M_1 = (Q_1, \Sigma, \delta_1, s_1, F_1)\) with \(L(M_1) = A\)
• there exists \(M_2 = (Q_2, \Sigma, \delta_2, s_2, F_2)\) with \(L(M_2) = B\)
• since A and B are regular, we can build a DFA \(M_3\) s.t. \(L(M_3) = A \cap B\).
• let \(M_3 = (Q_3, \Sigma, \delta_3, s_3, F_3)\)
• \(Q_3 = Q_1 \times Q_2 = \{(p, q) | p \in Q_1, q \in Q_2 \}\)
• \(F_3 = F_1 \times F_2 = \{(p, q) | p \in F_1, q \in F_2 \}\)
• \(s_3 = (s_1, s_2)\)

• \(\delta_3: Q_3 \times \Sigma \to Q_3\)

  • \(\delta_3((p, q), a) = (\delta_1(p, a), \delta_2(q, a))\)

• extended transition function:

  • \(\hat{\delta_3}((p, q), \epsilon) = (p, q)\)
  • \(\hat{\delta_3}((p, q), xa) = \delta_3(\hat{\delta_3}((p, q), x), a)\)

Pf: \(L(M_3) = L(M_1) \cap L(M_2)\)

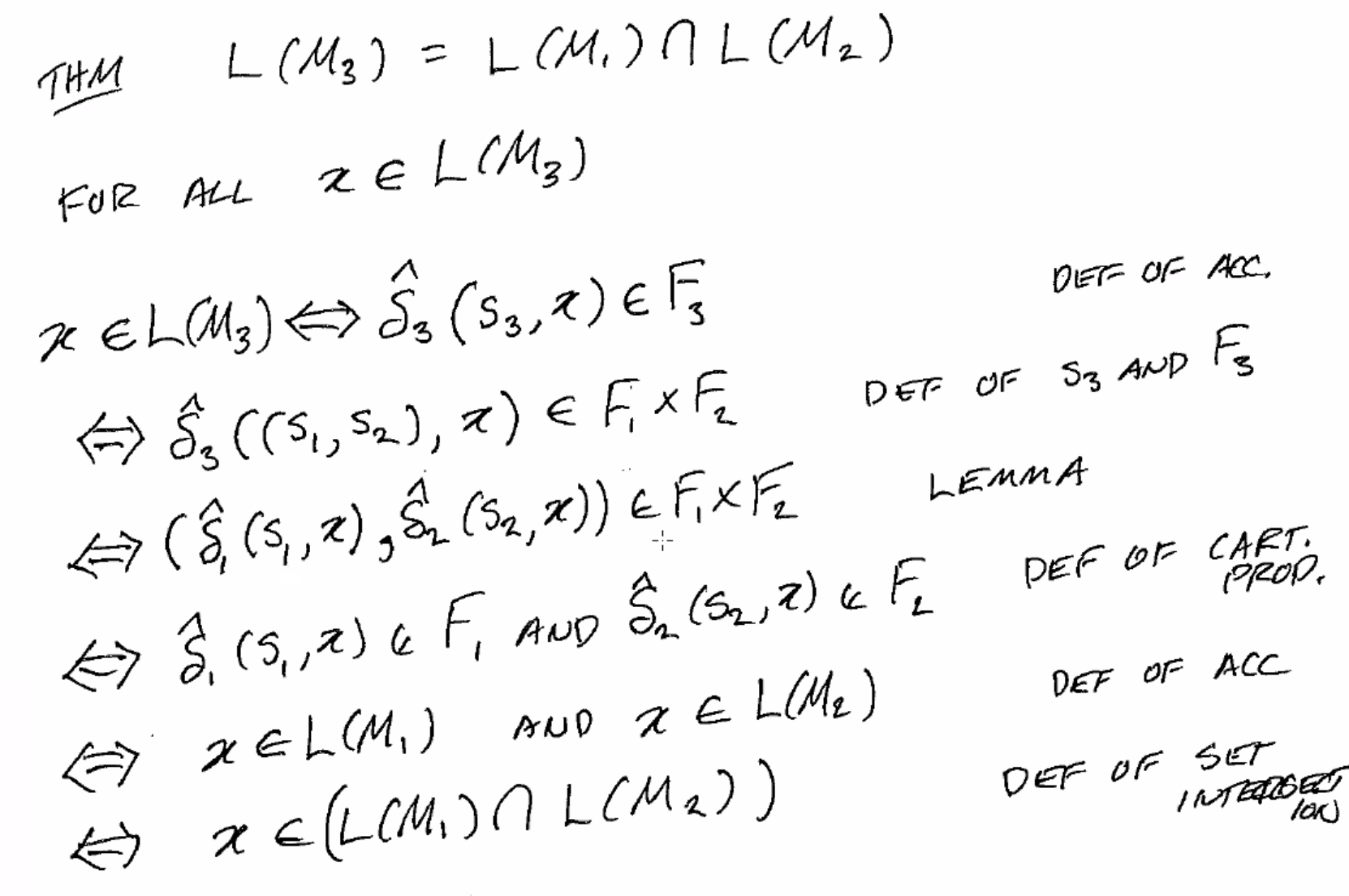
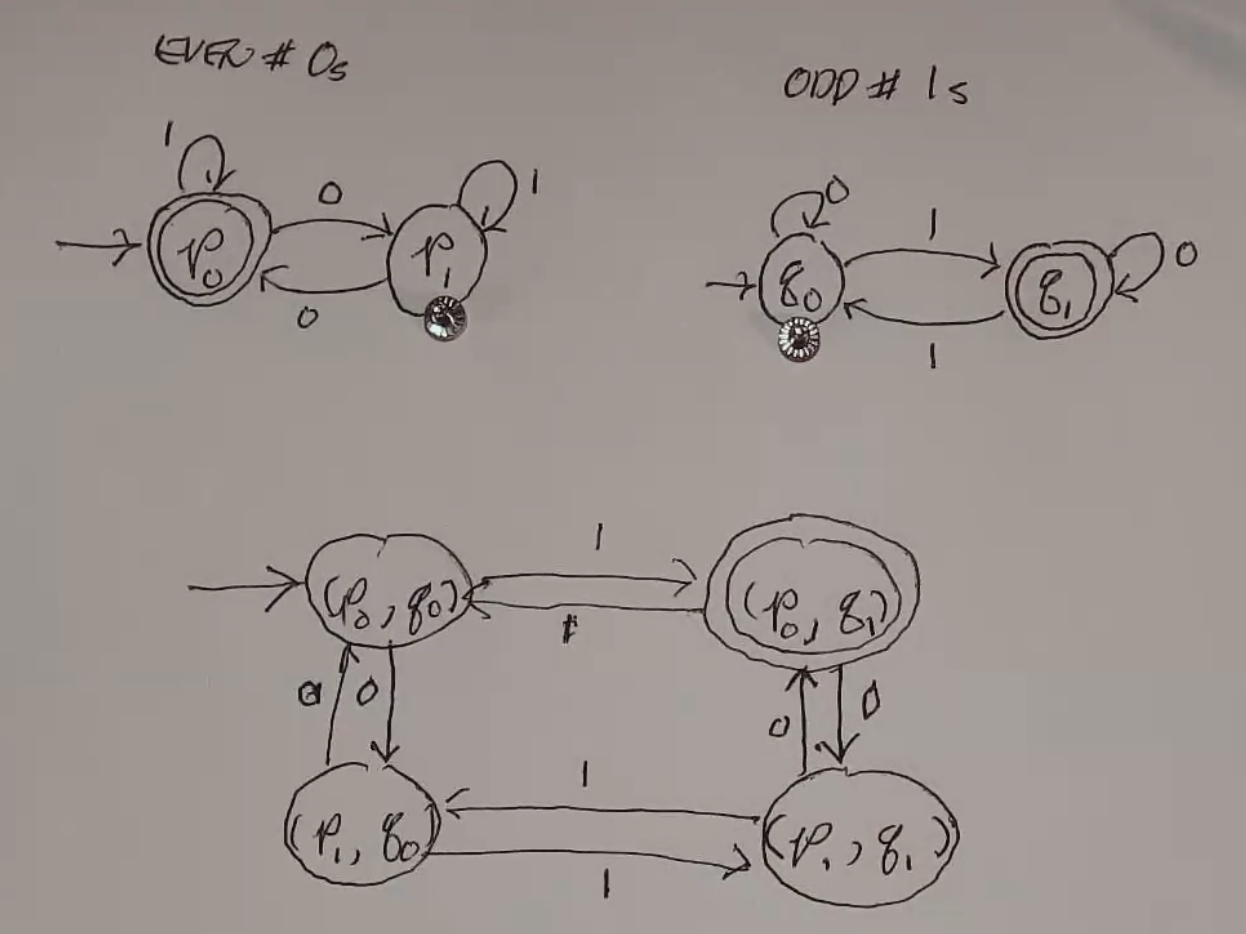
Ex: Given two machines that accept an even number of 0s and odd number of 1s, the intersection can be constructed as such:

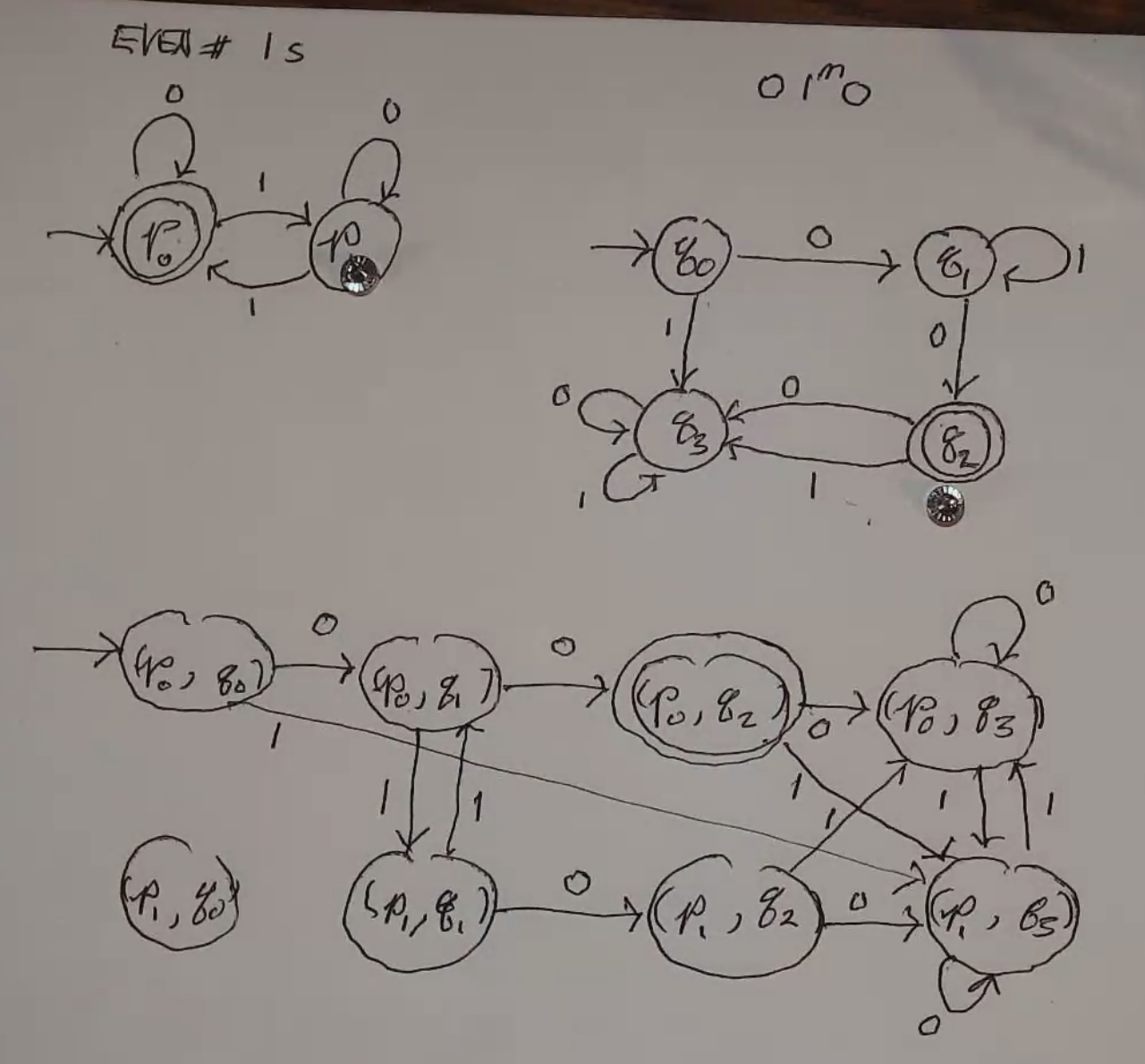
Ex: Even number of 1s and form \(01^m0\)

Note that there is no way into \((p_1, q_0)\).

Union

Thm: If languages A and B are regular, then \(A \cup B\) is regular.

• A is regular \(\implies \lnot A\) is regular
• B is regular \(\implies \lnot B\) is regular
• \(\lnot A \text{ and } \lnot B\) regular \(\implies \lnot A \cap \lnot B\) regular
• \(\lnot A \cap \lnot B\) regular implies \(\lnot (\lnot A \cap \lnot B)\) regular
• \(\lnot (\lnot A \cap \lnot B)\) regular implies \(A \cup B\) regular (demorgans).