Regular Expressions¶
Regular expressions over alphabet \(\Sigma\):

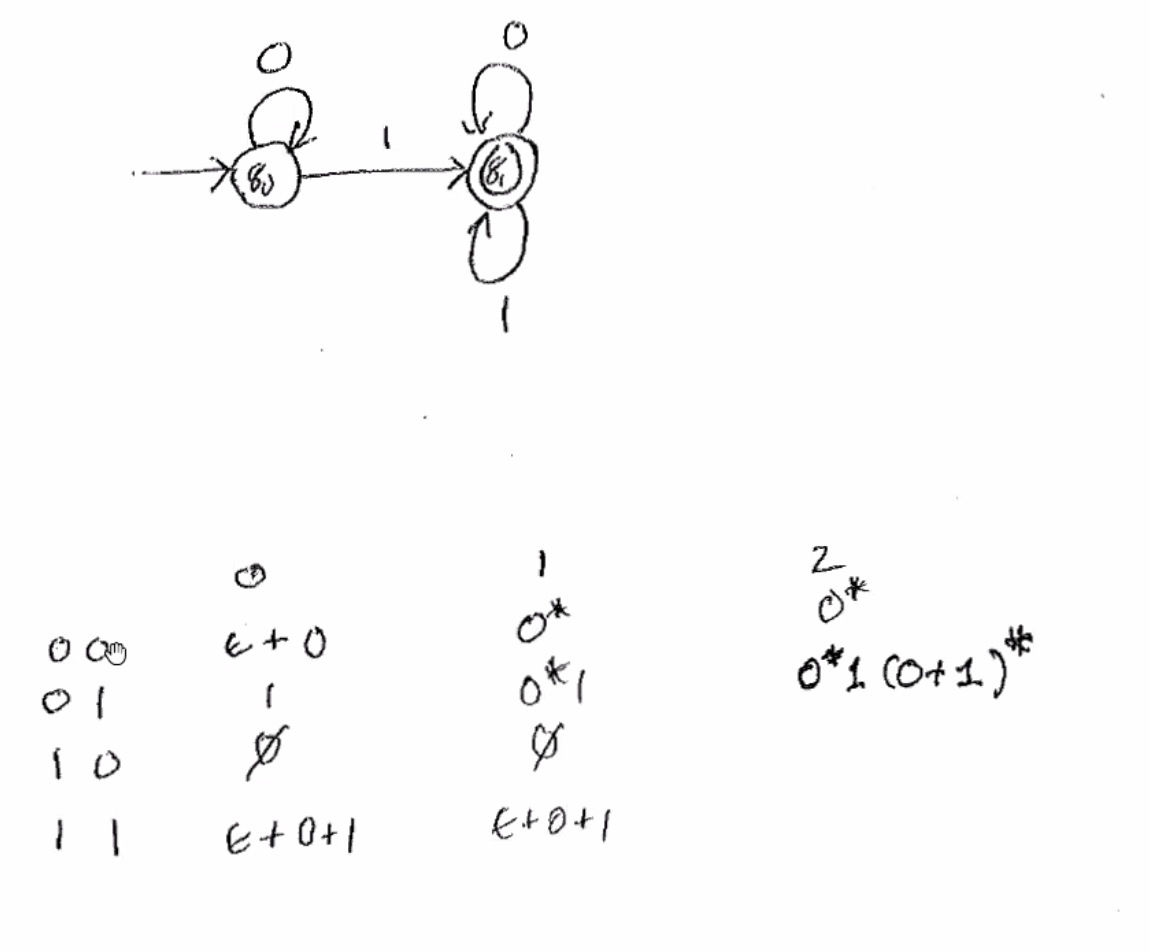
Ex. Begin with 0, end with 11: 0(0+1)*11
Ex. Contains at least 2 1s: (0+1)* 1 (0+1)* 1 (0+1)* or 0* 1 0* 1 (0+1)*
Note
a+ is often used as an abbreviation for aa*
Ex. Contains the substring 111: (0+1)* 111 (0+1)*
Ex. Even length: ((0+1)(0+1))*
Ex. Odd length: (0+1)((0+1)(0+1))*
Ex. Strings that don’t end with 01: e + 1 + (0+1)*0 + (0+1)*11 - it’s hard to exclude things!
Ex. Every 0 is followed by at least one 1: 1* (011*)*
Ex. 3rd symbol from right is 1: (0+1)* 1 (0+1)(0+1)
Ex. Contains both 01 and 10. ((0+1)* 01 (0+1)* 10 (0+1)*) + ((0+1)* 10 (0+1)* 01 (0+1)*)
Ex. Not containing 00. (1+01)*(0+e)
Ex. At most 1 00. Consider: (1+01)* has no 00 and does not end w/ 0, (1+10)* has no 00 and does not
start w/ 0. So exactly 1 occurance of 00: (1+01)* 00 (1+10)*, and up to 1 is just the combination:
(1+01)*(0+e) + (1+01)* 00 (1+10)*.
Ex. Not containing 110. 0* (100*)* 111*
Kleene’s Thm¶
For every regular expression, there is an equivalent \(\epsilon\)-NFA.
Use strong induction to prove:
- NFAs for regexes of length 1:
- let the building blocks have a unique accept state
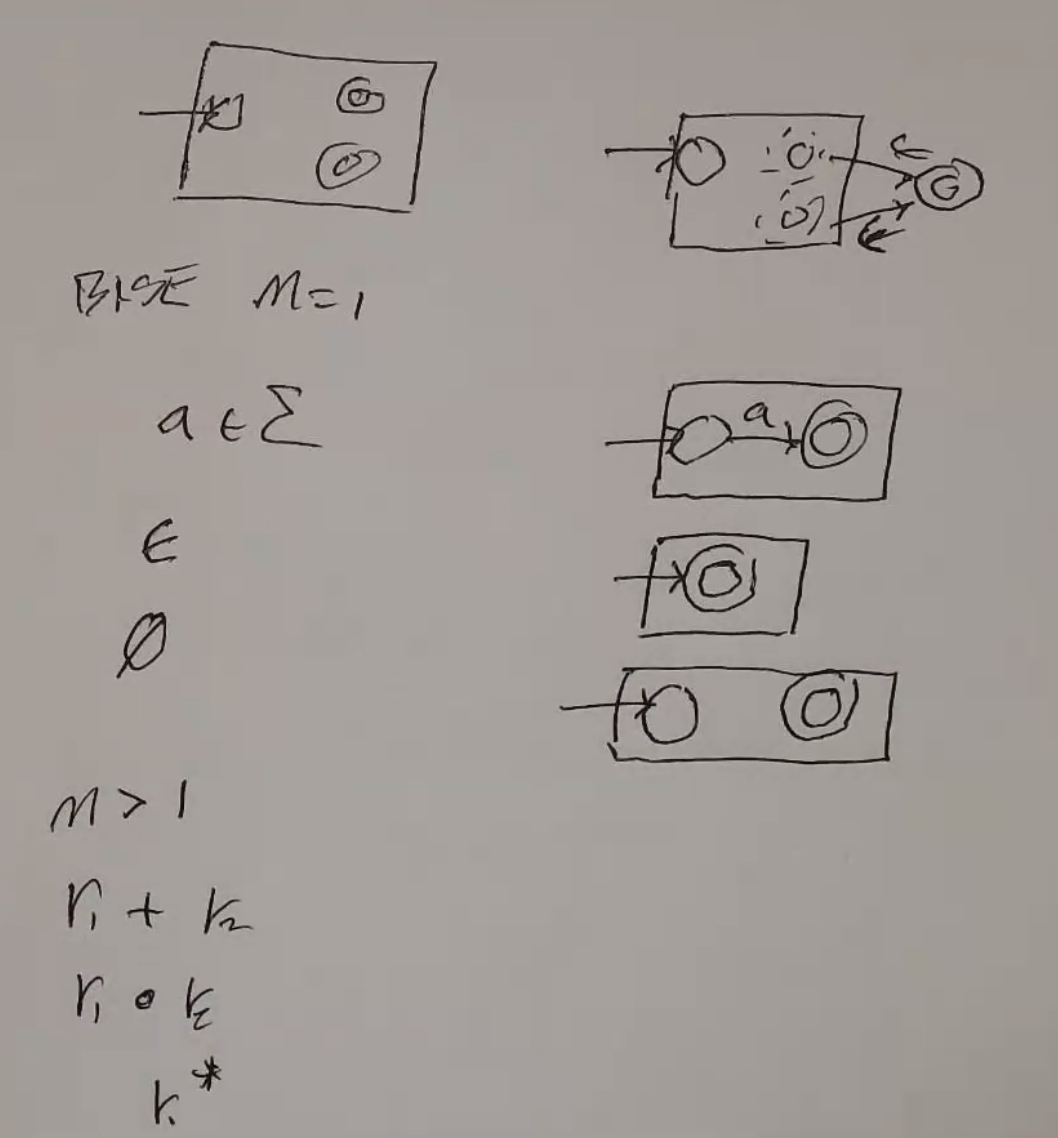
- All regexes longer than length 1 are:
- two smaller regexes with addition
- two smaller regexes with concatenation
- one smaller regex starred
- IS: prove S(M) is true given that S(i) is true for all i < M.
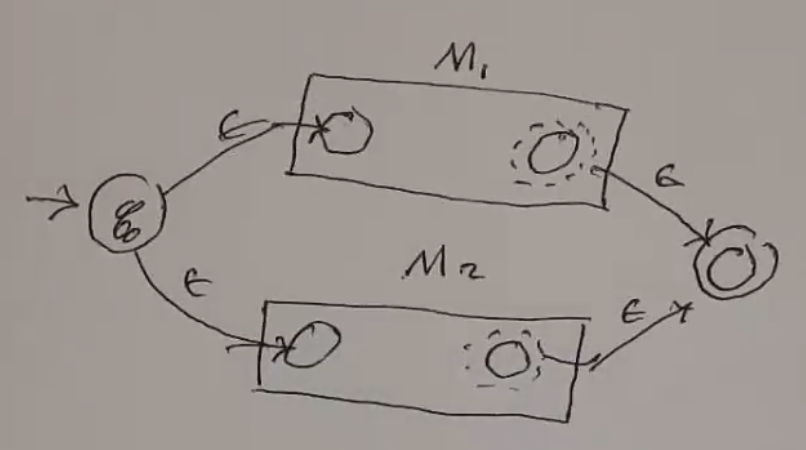
- Case: \(r = r_1 + r_2\)
- since \(r_1, r_2\) are smaller than r, there exists an \(\epsilon\)-NFA with a single unique accept state for each. (IH)
- Let these be \(M_1\) and \(M_2\).
- By adding a new start state, e-steps from that start state to the start states of of \(M_1\) and \(M_2\), and e-steps from the accept states to a new unique accept state, it is possible to construct an \(\epsilon\)-NFA to accept \(r_1 + r_2\).
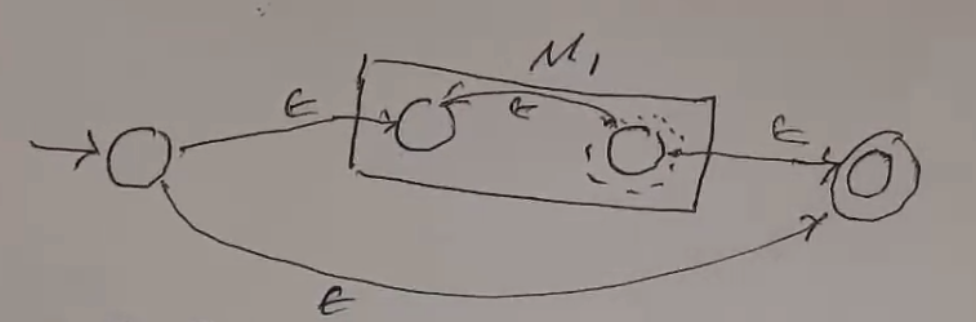
- Case: \(r = r_1 \cdot r_2\) (concatenate)
- since \(r_1, r_2\) are smaller than r, there exists an \(\epsilon\)-NFA with a single unique accept state for each. (IH)
- Let these be \(M_1\) and \(M_2\).
- By adding an e-step from the accept state of M1 to the start state of M2, it is possible to construct an \(\epsilon\)-NFA to accept \(r_1 + r_2\).

- Case: \(r = r_1*\)
- since \(r_1\) is smaller than r, there exists an \(\epsilon\)-NFA with a single unique accept state. (IH)
- Let this be \(M_1\).
- By adding an e-step from the old accept state to the old start state, from the old accept state to a new accept state, and the new start state to a new accept state.
- QED.
The Other Way Around¶
Thm. Given a DFA, NFA, or e-NFA, there exists a regex that accepts the language of that FA.

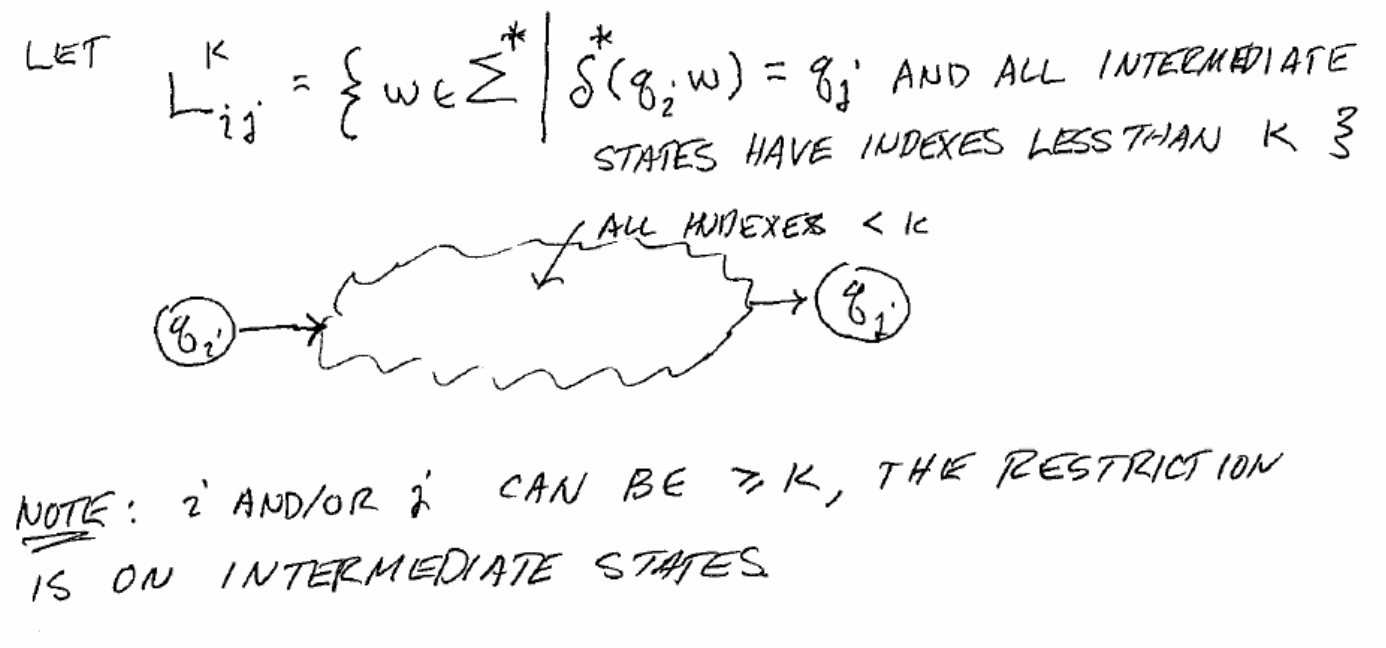
Define \(L_{ij}^k\) as the set of strings that will move the DFA from \(q_i\) to \(q_j\), where all intermediate states’ indices are < k.
Now we can define L(M) as the union of all ways to get from \(q_0\) to an accept state for each accept state:
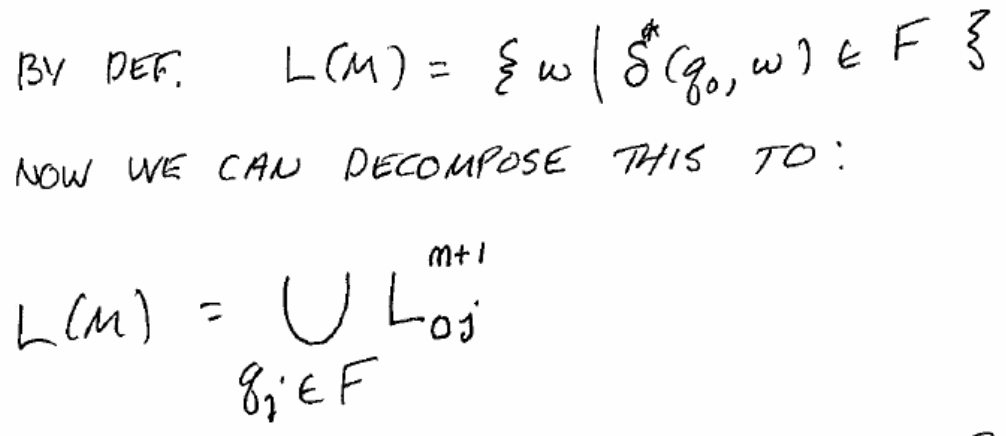


(Above: let’s call this regex for \(L_{ij}^k\) \(r_{ij}^k\))
The induction:
- base case. Since k = 0, this means only direct transitions:


this produces two cases: if the path does not encounter k, or if it does:

And if it does, it must have a first time it enters k and the last time it exits k, and anything in between must be k to k, where all intermediate nodes are < k:
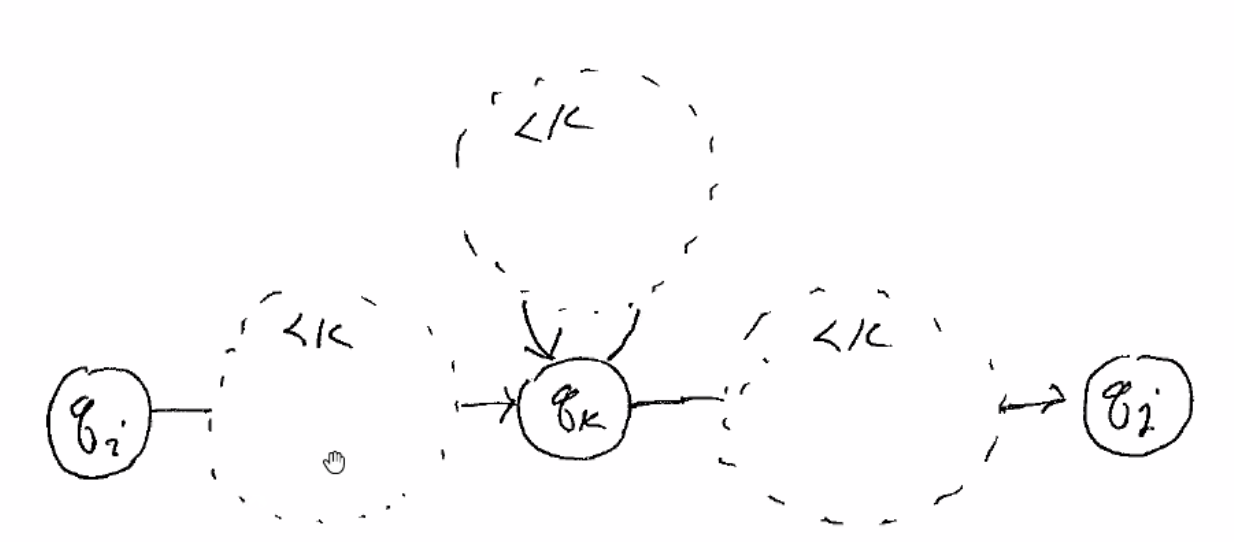
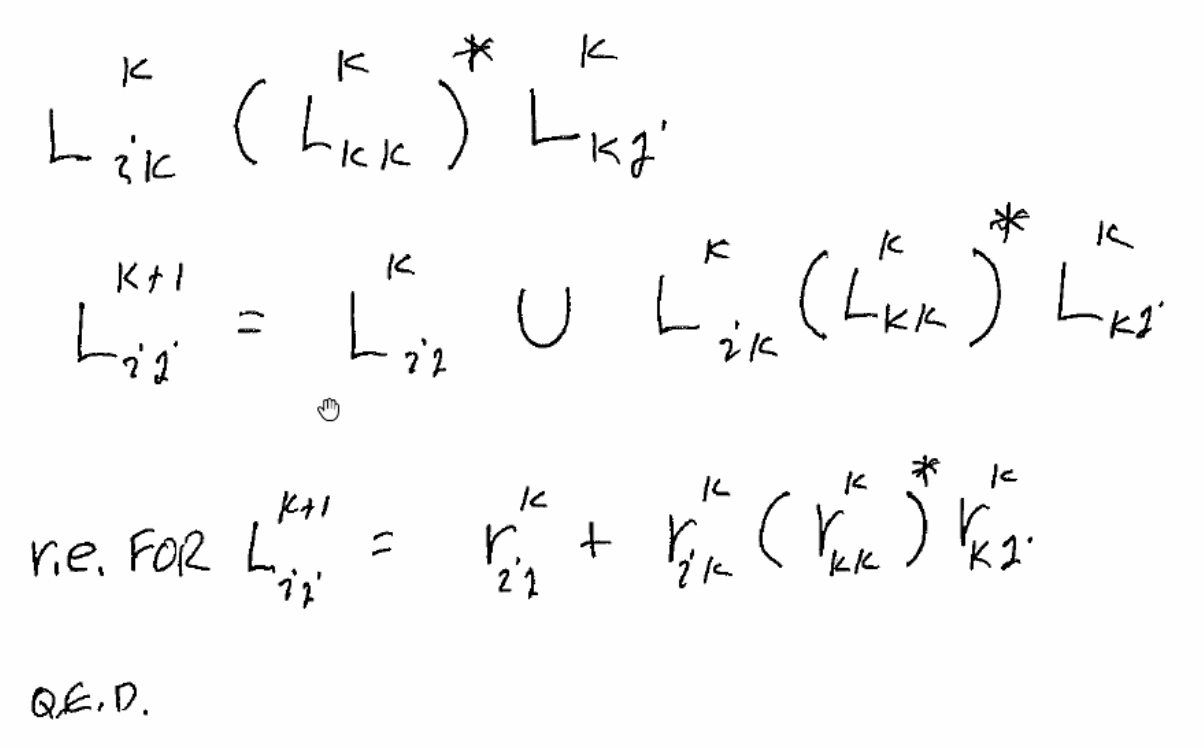
Now, we can expand this regex to:
\(\sum_{q_j \in F} r^k_{0j}\).