Pumping Lemma¶
If a language L is regular, then:
(P): There exists a \(p \geq 0\) s.t. for any string \(s \in L\) with \(|s| \geq p\), there exist strings \(xyz\) s.t. \(s = xyz, y \neq \epsilon, |xy| \leq p\), and for all \(i \geq 0\), the string \(xy^iz \in L\).
“there exists a non-empty string (y) within the first p characters (3rd constraint) that can be pumped, with the resulting string still being in the language.”
The contrapositive of this (\(\lnot P \implies\) L is not regular) is used to prove that a language is not regular.
(not P): For all \(p \geq 0\) there exists a string \(s \in L\) with \(|s| \geq p\), and for all \(x, y, z\) such that \(xyz = s, y \neq \epsilon, |xy| \leq p\) there exists an \(i \geq 0\) such that \(xy^iz \notin L\).
You can use this adversarial game to prove the contrapositive:
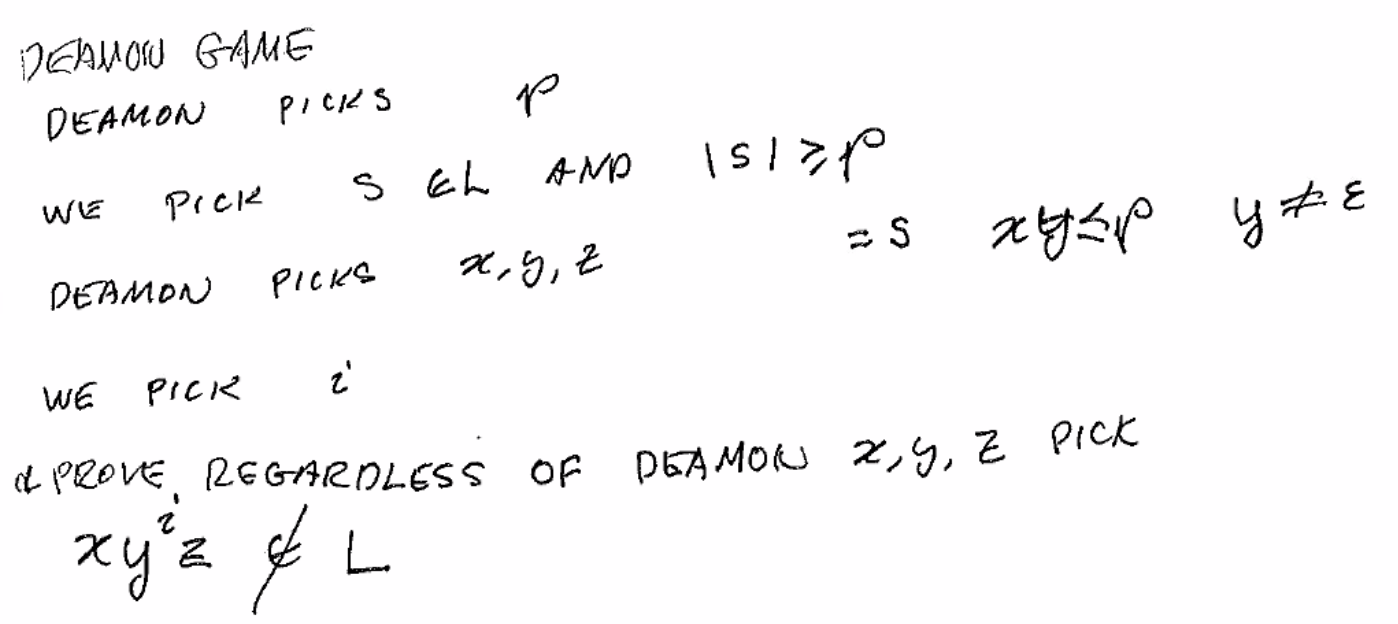
Proof¶
Given a DFA with p states, processing any string with length \(m \geq p\) means the machine will visit at least p + 1 states. By the pigeonhole principle, at least one state will be revisited.
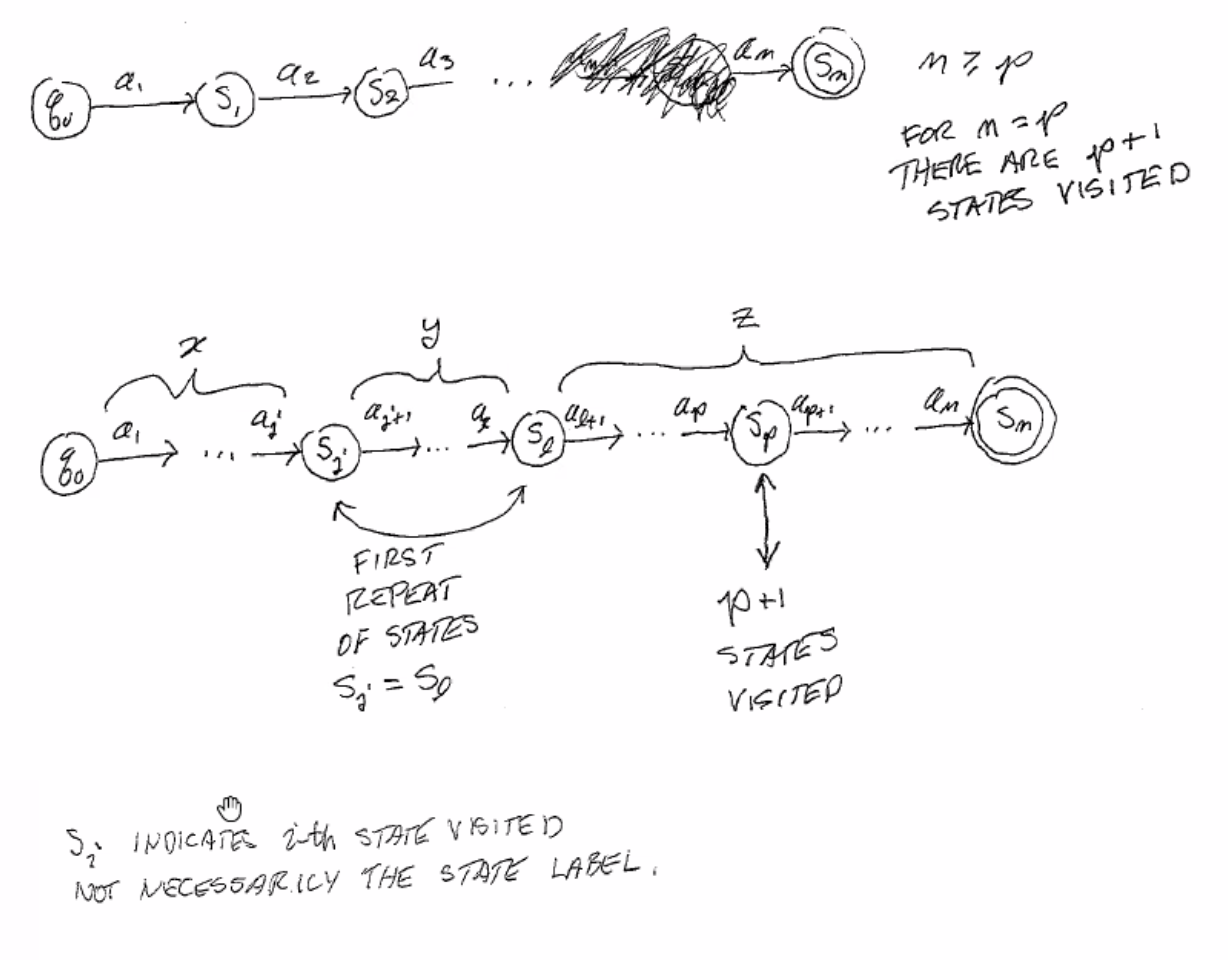
Notice that the string that causes the DFA to go from \(s_j\) to \(s_l\) can be repeated infinitely, since they are a loop.
Examples¶
Ex 1¶
\(A = \{ 0^m1^m | m \geq 0 \}\) is not regular.
Use the demon game as a valid proof:
- Demon picks p
- we pick \(s \in L\) and \(|s| \geq p\)
- \(s = 0^p1^p\)
- demon picks partition \(x, y, z\) s.t. \(xyz = s, |xy| \leq p, y \neq \epsilon\)
- we show any partition that satisfies these conditions cannot be pumped for some \(i \geq 0\)
- since \(|xy| \leq p, y \neq \epsilon\) and we chose \(s = 0^p1^p\), y must be one or more 0s
- choose \(i = 2\): this causes \(xy^2z\) to have more 0s than 1s and not be in the language
- QED
Ex 2¶
\(L = \{ w | \text{ # of 0s = # of 1s} \}\) is not regular.
Abbreviated demon argument:
- \(p\)
- \(s = 0^p 1^p\)
- for any partition \(x, y, z\) s.t. \(xyz = s, |xy| \leq p, y \neq \epsilon\): (same argument as before)
- y must be made of 1 or more 0s
- choose \(i = 2\): this causes \(xy^2z\) to have more 0s than 1s and not be in the language
- QED
Ex 3¶
\(L = \{ 1^j 0^i | j < i \}\) is not regular
- \(p\)
- \(s = 1^p 0^{p+1}\) (conditions: \(s \in L, |s| = 2p+1 \geq p\))
- for any partition \(x, y, z\) s.t. \(xyz = s, |xy| \leq p, y \neq \epsilon\):
- y must be made of 1 or more 1s
- choose \(i = 2\): this causes \(xy^2z\) to have \(i \geq j\) and not be in the language
- QED
Ex 4¶
\(L = \{ 0^i 1^j | i > j \}\) is not regular
- Assume L is regular
- so the reverse of L is regular (closure under reverse)
- The reverse of L is not regular (ex 3)
- so L is not regular. QED.
Ex 5¶
\(L = \{ ww | w \in \{0, 1\}* \}\) is not regular
- \(p\)
- \(s = 0^p10^p1\)
- \(|s| = 2p+2 \geq p, s \in L\)
- \(xyz = 0^p10^p1\) s.t. \(|xy| \leq p, |y| > 1\)
- if \(i = 2\), \(xy^2z \notin L\).
- since then there will be more 0s before the first 1 than before the last one.
Ex 6¶
Palindrones ( \(L = \{ w | w = w^R \}\) ) are not regular.
- \(p\)
- \(s = 0^p 1 0^p\)
- \(|s| = 2p+1 \geq p, s \in L\)
- \(xyz = 0^p10^p\) s.t. \(|xy| \leq p, |y| > 1\)
- for any i ≥ 2, the new string of the form \(xy^iz\) will have more 0s before the 1 than after, and will no longer be in the language.
Ex 7¶
\(L = \{0^m1^n | m \neq n \}\) is not regular
- \(p\)
- \(s = 0^p1^{p+p!}\)
- \(xyz = 0^p1^{p+p!}\) s.t. \(|xy| \leq p, |y| > 1\)
- so y must be 1 or more 0s
- let the length of y be k, so \(xyz = 0^{p-k}0^k1^{p+p!}\)
- pick \(i = \frac{p!}{k}+1\)
- \(|y| = k\), so \(|y^i| = ki = k * \frac{p!}{k}+1 = p!+k\)
- then \(xyz = 0^{p-k}0^{p!+k}1^{p+p!}\)
- \(=0^{p+p!}1^{p+p!} \notin L\).
Ex 7b¶
Alternatively, assume L is regular.
- Then \(\lnot L\) is regular (closed on complement)
- Then \(\lnot L \cap 0^*1^*\) is regular (closed on intersection)
- That language is \(\{ 0^m1^n | m=n \}\), which is not regular - contradiction!
Ex 8¶
\(L = \{ 1^{n^2} | n \geq 0 \}\) is not regular
- \(p\)
- \(s = 1^{p^2}\)
- \(xyz = s\) s.t. \(|xy| \leq p, |y| > 1\)
- let i = 2, then:
- \(|xy^2z| - |xyz| = |y| \leq p\)
- \(|xy^2z| \leq p^2+p\)
- \(p^2 < |xy^2z| \leq p^2 + p < (p+1)^2\), so \(s \notin L\).
Ex 9¶
\(L = \{ 0^{2^n} | n \geq 1 \}\) is not regular
- \(p\)
- \(s = 0^{2^p}\)
- \(xyz = s\) s.t. \(|xy| \leq p, |y| > 1\)
- let \(|x| = a, |y| = b, |z| = c, 0 < b \leq p, a+b=p\)
- let i = 2, \(s' = xy^2z\), then:
- \(|xy^2z| = 2^p+b\)
- \(2^p+b \leq 2^p+p\)
- \(< 2^p+2^p\)
- \(= 2^{p+1}\)
- so \(|xy^2z|\) is not a power of 2, so \(s' \notin L\).
Ex 10¶
\(L = \{ a^{n!} | n \geq 0 \}\) is not regular
- \(p\)
- \(s = a^{p!}\)
- \(xyz = s\) s.t. \(|xy| \leq p, |y| > 1\)
- let \(|x| = j, |y| = m > 0, |z| = n, j+m+n = p!\)
- pick i s.t. \(|xy^iz| \neq q!\) for any q
- for any i, \(|xy^iz| = j+im+n = p!+(i-1)m\)
- pick \(i = (p+1)! + 1\), then \(|xy^iz| = p! (p+1)! m\)
- \(=p!(1+m(p+1))\), prove that this is not a factorial
- assume \(q! = p!(1+m(p+1))\)
- then dividing both sides by \(p!\): \(q(q-1)(q-2)...(p+2)(p+1) = (1+m(p+1))\)
- impossible because left is divisible by \(p+1\) and right side leaves remainder of 1.
- therefore \(p!(1+m(p+1))\) is not a factorial, so \(xy^iz \notin L\).
Ex 11¶
\(L = \{ 1^n | n \text{ is prime} \}\)
- \(p\)
- \(s = 1^{p'}\) where \(p'\) is a prime larger than p
- \(xyz = s\) s.t. \(|xy| \leq p, |y| > 1\)
- let \(x = 1^a, a \geq 0\)
- let \(y = 1^b, b > 0\)
- let \(z = 1^c, c \geq 0\)
- where \(a+b+c = p'\)
- so the claim is \(a + ib + c\) is a prime for all i
- let \(i = a + 2b + c + 2\)
- then \(a + ib + c = (b+1)(a+2b+c)\)
- this is a factor of two numbers, and so not a prime
- therefore \(xy^iz \notin L\).