Context-Free Languages

CFLs are more powerful than regular languages! You can use them to do things like balance parens.

Ex. palindromes, \(0^n1^n\), balanced parens, etc.

Context-Free Grammars

CFGs are used to generate CFLs.

Definition

\(G = (N, \Sigma, P, S)\)

Note

N (“nonterminals”) is sometimes V (“variables”), and P (“productions”) is sometimes R (“rules”)

• \(N\) is a finite set (nonterminal symbols/variables)

• \(\Sigma\) is a finite set (terminal symbols, disjoint from N)

  • \(N \cap \Sigma = \emptyset\)

• \(P\) is a finite subset of \(N \times (N \cup \Sigma)^*\) (productions)
• \(S \in N\) is the start symbol/variable

Convention

• \(A, B, C...\) = nonterminals
• \(a, b, c...\) = terminals
• \(\alpha, \beta, \gamma...\) = strings in \((N \cup \Sigma)^*\)
• \(A \to \alpha\) for \((A, \alpha)\)
• \(A \to \alpha_1, A \to \alpha_2, A \to \alpha_3\) = \(A \to \alpha_1 | \alpha_2 | \alpha_3\)

A grammar can be abbreviated as a list of rules. The nonterminals can be found on the left, the rules are listed, the terminals are the states on the right that are not on the left, and the start state is the top nonterminal.

Examples

Note

For these examples, \(\to\) will be expressed as := and \(\epsilon\) as e.

Ex 1

\(a^nb^n\)

Formally:

• \(G = (N, \Sigma, P, S)\)
• \(N = \{S\}\)
• \(\Sigma = \{a, b\}\)
• \(P = \{S \to aSb, S \to \epsilon\}\)
• \(S = S\)

Abbreviated:

S := a S b | e

Ex. \(a^3b^3\) can be S := aSb := aaSbb := aaaSbbb := aaabbb.

Ex 2

Even length palindromes.

S := a S a | b S b | e

Ex. aabbaa can be S := aSa := aaSaa := aabSbaa := aabbaa.

Ex 3

Odd length palindromes.

S := a S a | b S b | a | b

Ex. aababaa can be S := aSa := aaSaa := aabSbaa := aababaa.

Ex 4

The set of strings over {a, b} such that the reversal of a string is the string with a’s and b’s swapped

S := a S b | b S a | e

Ex 5

The set of even length strings

S := a T | b T | e
T := a S | b S

OR

S := aaS | abS | baS | bbS | e

Ex 6

Even length with two middle symbols the same

S := a S a | a S b | b S a | b S b | aa | bb

Ex 7

Odd length with first, middle, and last symbols the same

S := a T a | b U b
T := a T a | a T b | b T a | b T b | a
U := a U a | a U b | b U a | b U b | b

Ex 8

Equal number of a’s and b’s

S := a S b | b S a | S S | e

Ex 9

Palindromes

S := a S a | b S b | a | b | e

Ex 10

Balanced parentheses

S := ( S ) | S S | e

Ex 11

\(\{0, 1\}^*\)

S := 0 S | 1 S | e

Special Constructions

• Right Linear

  • A := x B | x where \(x \in \Sigma^*\)

• Strongly Right Linear

  • A := x B | e where \(x \in \Sigma\)

• Left/Strongly Left Linear are similar.

  • All the linear constructions generate the regular languages!

DFA Relation

Since the linear constructions generate the regular languages, they must have an associated DFA:

\(M = (Q, \Sigma, \delta, s, F)\)

• Make a variable for each state: \(V = \{V_i | q_i \in Q\}\)
• \(\Sigma = \Sigma\)

• For each \(\delta(q_i, a) \to q_j\) where \(a \in \Sigma\):

  • make a rule \(V_i \to a V_j\)

• For each \(q_i \in F\):

  • make a rule \(V_i \to \epsilon\)

• \(S = V_0\)

Ex. Use this method on the language of an odd number of 0s, even number of 1s.

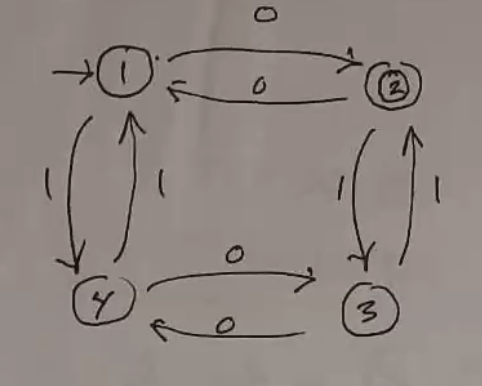
V1 := 0 V2 | 1 V4
V2 := 0 V1 | 1 V3 | e
V3 := 0 V4 | 1 V2
V4 := 0 V3 | 1 V1

Closure

Given:

• \(G_1 = (N_1, \Sigma, P_1, S_1)\)
• \(G_2 = (N_2, \Sigma, P_2, S_2)\)

Union

• \(G = (N, \Sigma, P, S)\)
• \(N = N_1 \cup N_2 \cup \{S\}\)
• \(P = P_1 \cup P_2 \cup \{S \to S_1, S \to S_2\}\)
• \(S = S\)

Concatenation

• \(G = (N, \Sigma, P, S)\)
• \(N = N_1 \cup N_2 \cup \{S\}\)
• \(P = P_1 \cup P_2 \cup \{S \to S_1 S_2\}\)
• \(S = S\)

Kleene Star

(Examining \(G_1^*\))

• \(G = (N, \Sigma, P, S)\)
• \(N = N_1 \cup \{S\}\)
• \(P = P_1 \cup \{S \to \epsilon, S \to S_1S\}\)
• \(S = S\)

Intersection (Not)

CFLs are not closed under intersection! Counterexample:

• \(a^nb^nc^n\) is not a CFL

• \(\{a^mb^mc^n | m,n \geq 0\}\) is a CFL

  • Pf: See CFG 1 below

• \(\{a^mb^nc^n | m,n \geq 0\}\) is a CFL

  • Pf: See CFG 2 below

• \(\{a^mb^nc^n | m,n \geq 0\} \cap \{a^mb^mc^n | m,n \geq 0\} = a^nb^nc^n\) which is not a CFL.

CFG 1
S := A B
A := a A b | e
B := c B   | e

CFG 2
S := A B
A := a A   | e
B := b B c | e

Chomsky Normal Form

A special form where all rules are of the form A := BC | a (where \(A, B, C \in N\) and \(a \in \Sigma\)).

Thm. For any CFG G, there is a CFG G’ in CNF s.t. \(L(G')=L(G) - \epsilon\).

Converting to CNF

Step 1: Get rid of epsilon-rules and unit-rules

Step 2: Make everything either go to one terminal or multiple nonterminals

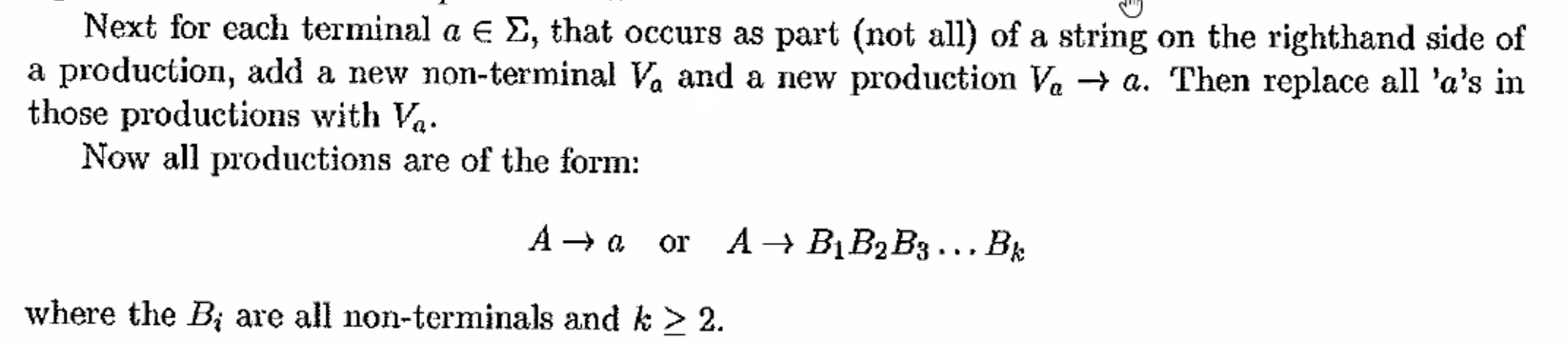
Step 3: Make every run of 2+ nonterminals just 2 nonterminals.

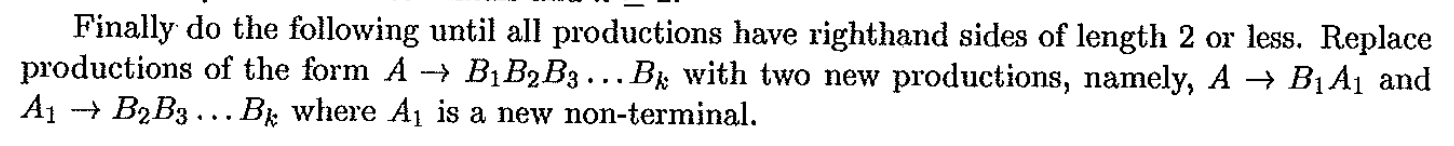
Ex.

\(L = \{a^nb^n | n \geq 1\}\)

0.
S := a S b | e

1. add S := a b
S := a S b | e | a b

2. Remove e-productions
S := a S b | a b

3. Give each terminal a nonterminal
S := a S b | a b
A := a
B := b

4. Replace nonterminals on the right
S := A S B | A B
A := a
B := b

5. Replace >2 nonterminals
S  := A S2 | A B
S2 := S B
A  := a
B  := b

Ex.

Balanced parentheses.

0.
S := ( S ) | S S | e

1. add S := ( ) and remove epsilon
S := ( S ) | S S | ( )

2. make each terminal a nonterminal
S := A S B | S S | A B
A := (
B := )

3. Replace runs of >2 nonterminals
S  := A S2 | S S | A B
S2 := S B
A  := (
B  := )

A more complex example can be found on Canvas.

Pumping Lemma for CFLs

For every CFL L, there exists a \(p \geq 0\) s.t. every \(z \in L\) of length \(\geq p\) can be divided into five substrings \(z = uvwxy\) such that \(vx \neq \epsilon\) and \(|vwx| \leq p\), and for all \(i \geq 0\), \(uv^iwx^iy \in L\).

In English: every sufficiently long string can be divided into 5 segements such that the middle 3 are not too long, and the second and fourth are both not empty, and no matter how much you pump the 2nd and 4th (simultaneously), the string stays in the language.

We can use this to prove that a language is not a CFL. We just need to show:

• for all \(p \geq 0\)
• there exists \(s \in L\) of length at least \(p\)
• such that for all \(uvwxy\) with \(z = uvwxy, vx\neq \epsilon, |vwx| \leq p\)
• there exists \(i\)
• such that \(uv^iwx^iy \notin L\).

We can use the adversary game again.

Proof

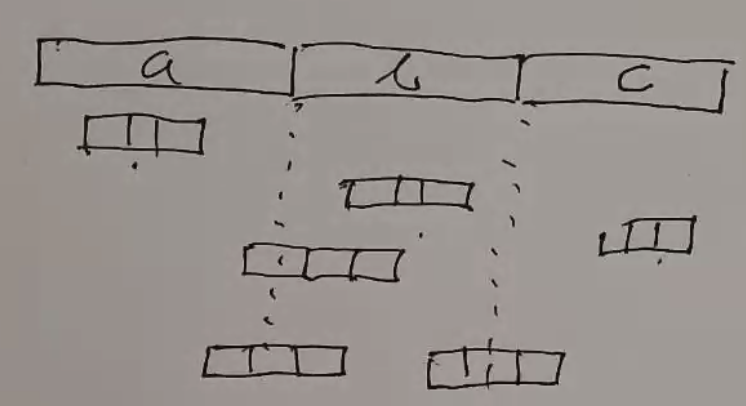
For any CFG, you can make a Chomsky derivation tree:

Each level may only double the number of nodes at most, since CNF only allows each nonterminal to go to 2 nodes.

For a derivation tree with \(2^n\) nodes on the bottom, the shortest path to the top must be at least \(n+1\) long.

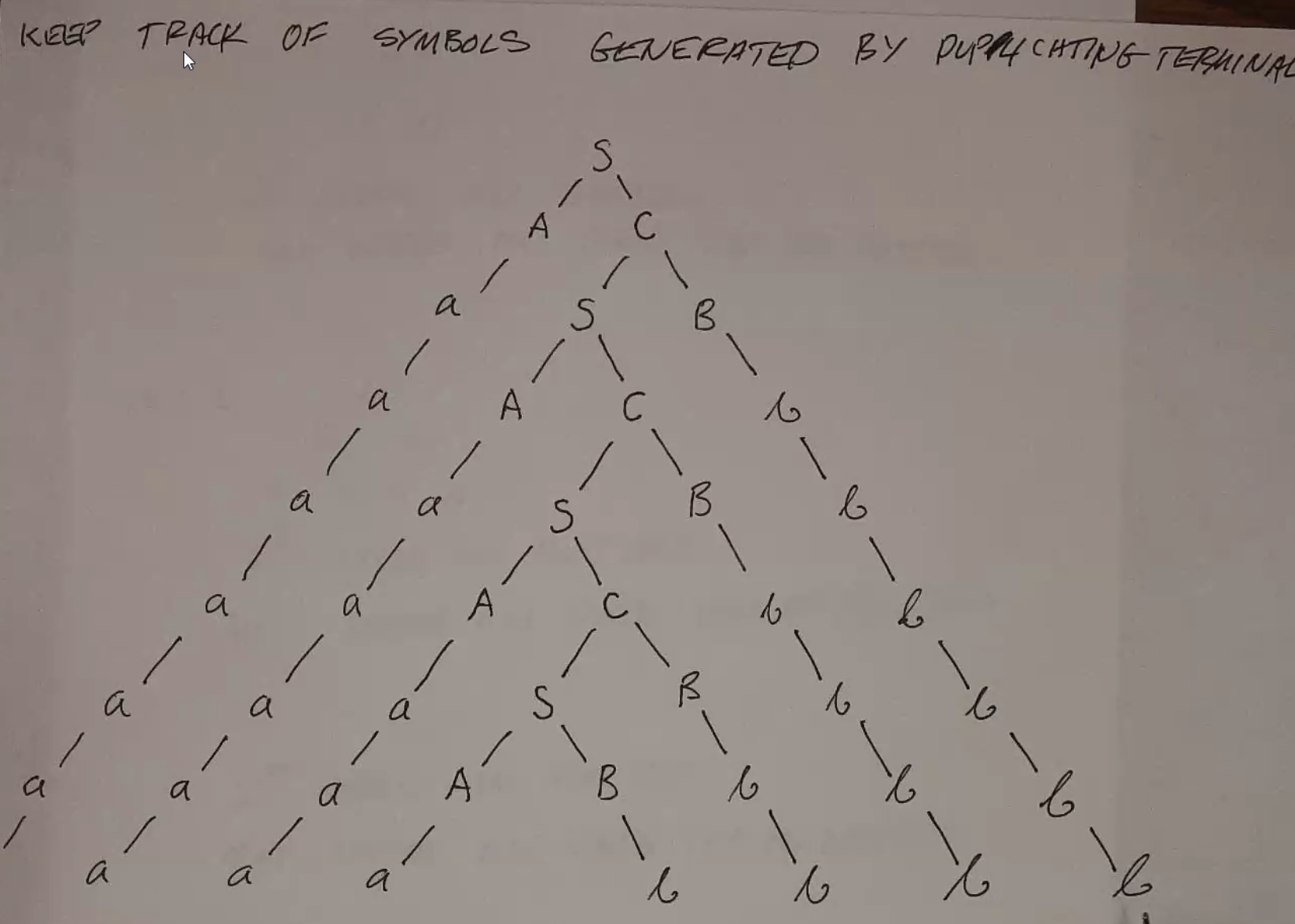
So for a grammar with \(n\) variables, the shortest path to the top must be at least \(n+1\) long.

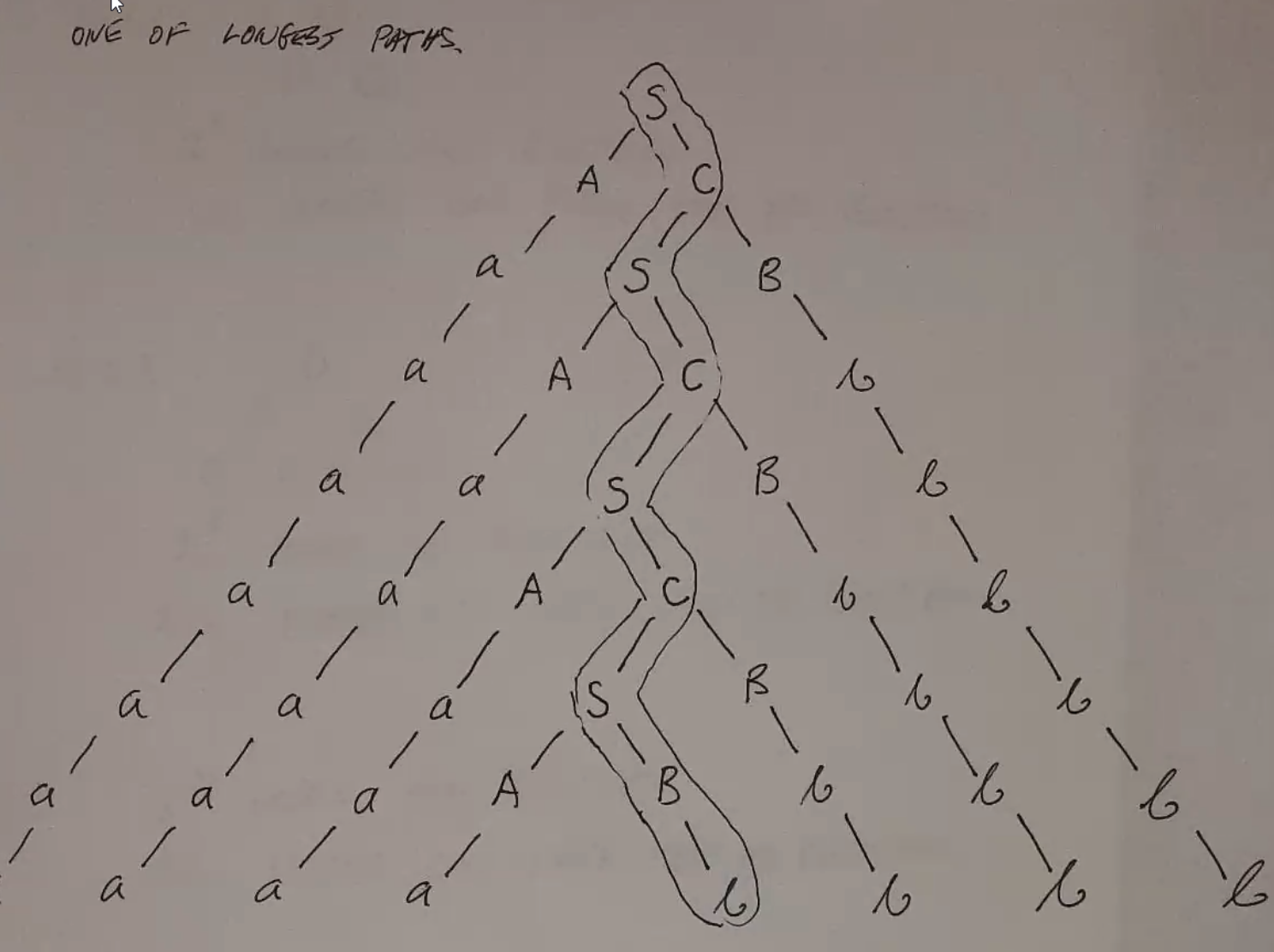
Which means, by the pigeonhole principle, at least 1 variable must be repeated along that path - you can pump along the first repeated variable:

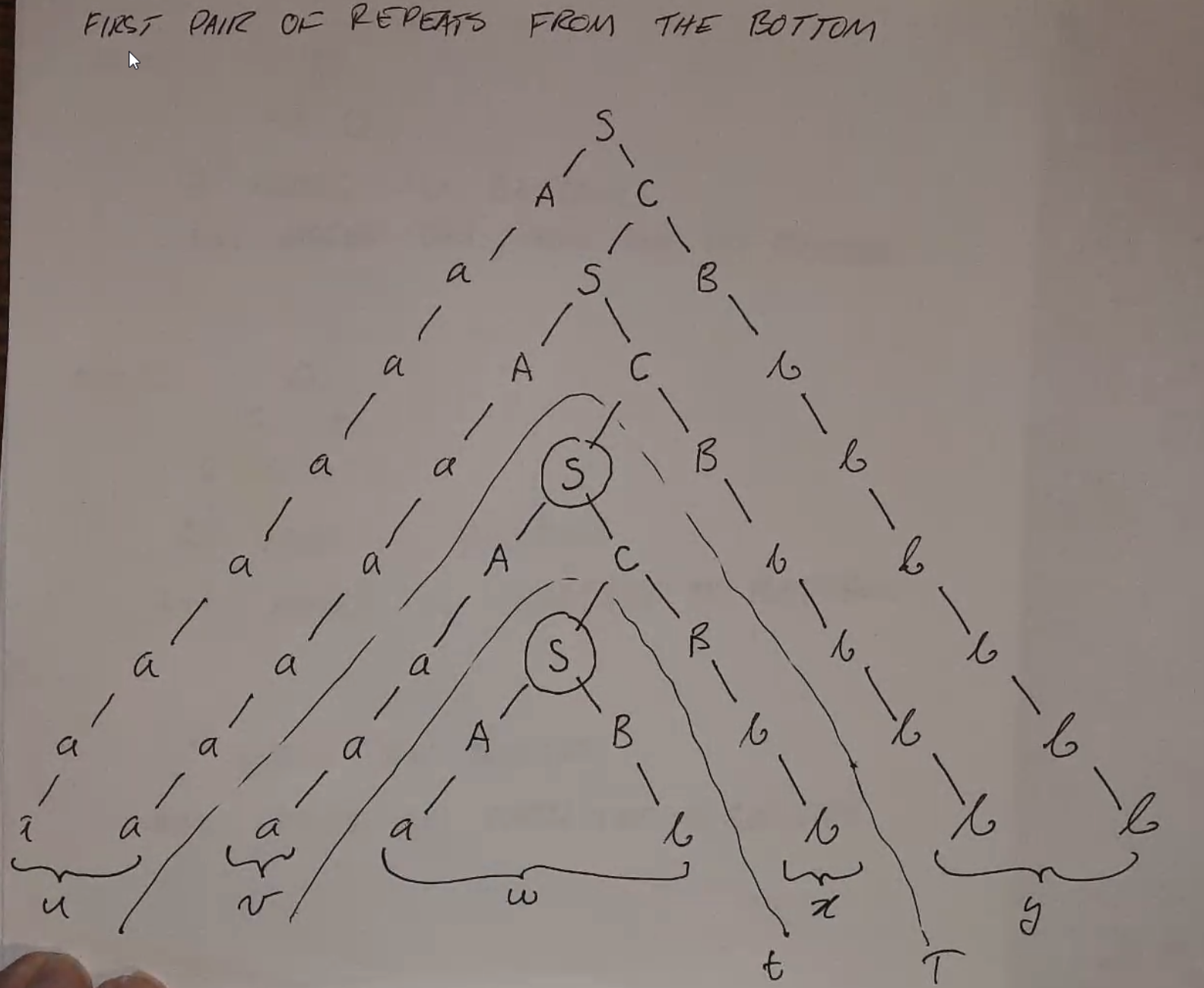
In this diagram, pumping v and x is roughly equivalent to removing the w portion and replacing its child with another of itself.

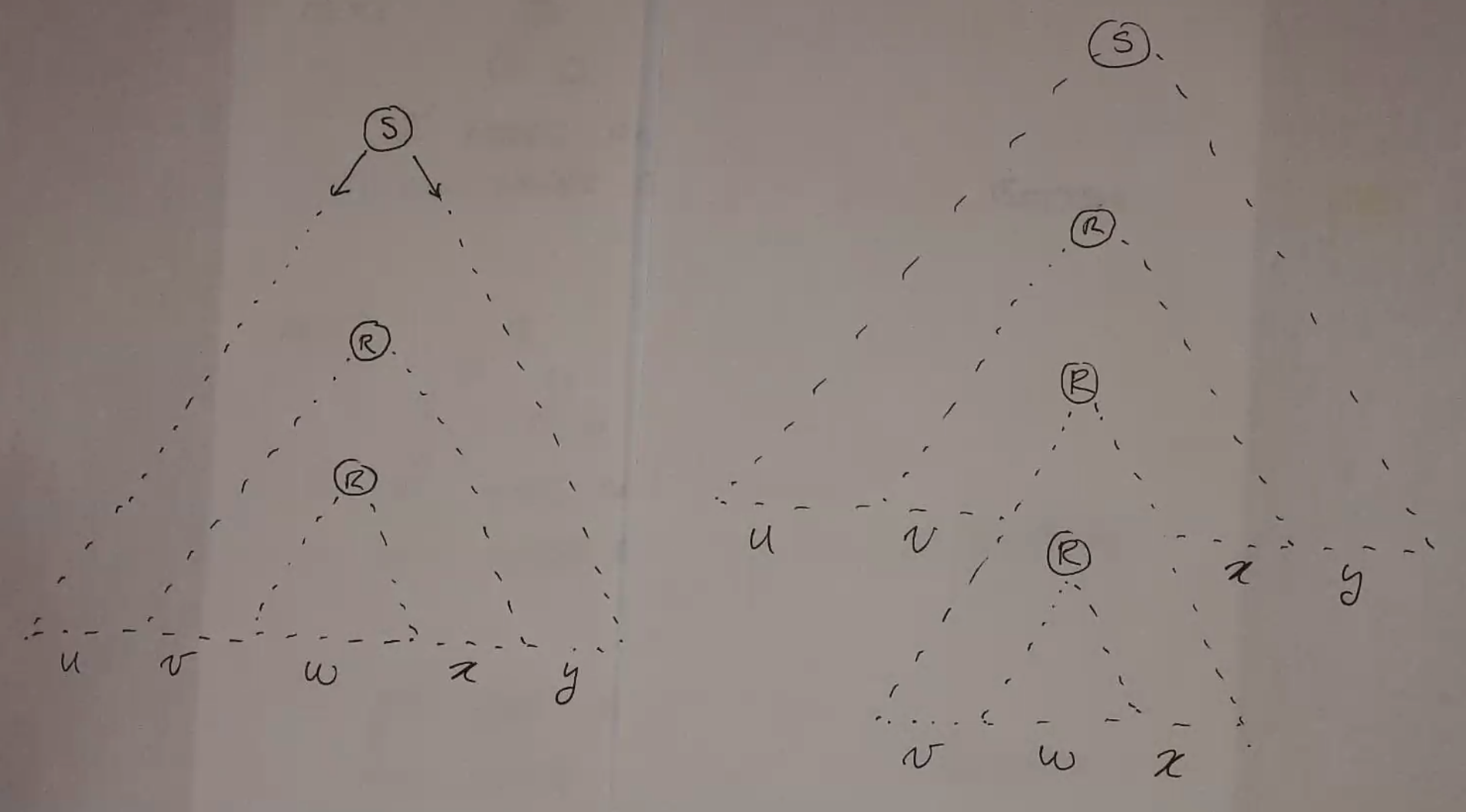
You can repeat this process to keep pumping. Alternatively, you can pump down by removing the v and x portions:

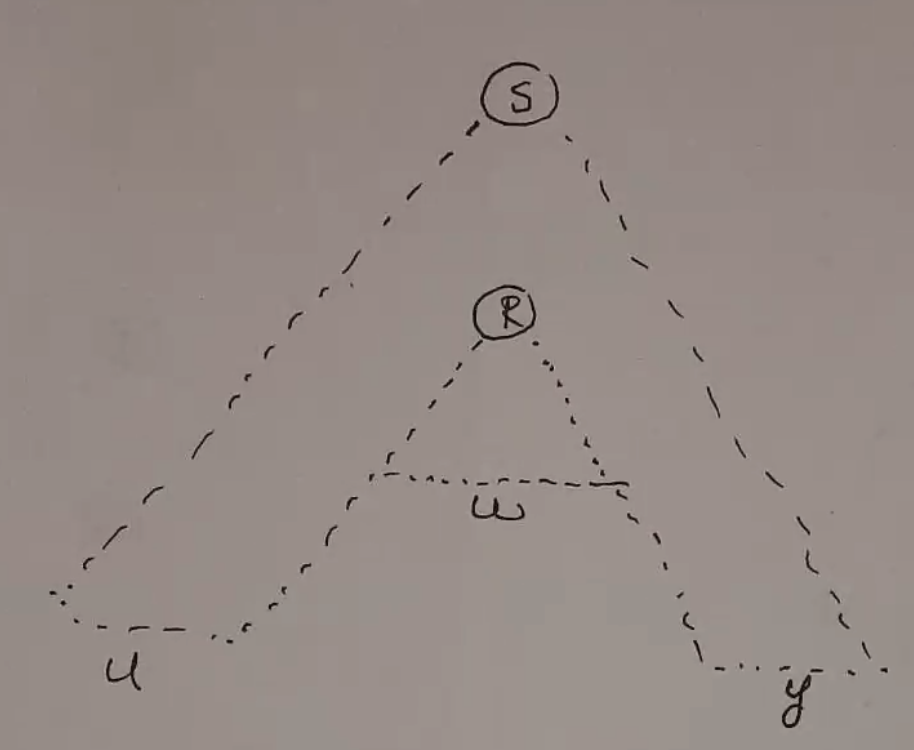
If either v or x is empty, it looks like this:

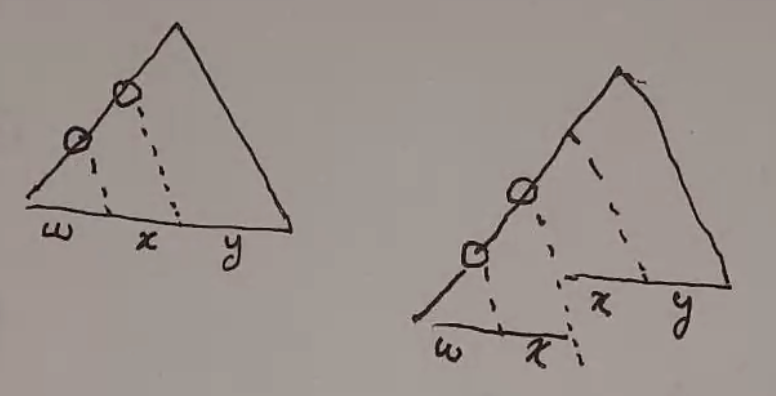
Ex 1

\(L = \{a^nb^nc^n | n \geq 0\}\)

• \(p\)
• \(s = a^pb^pc^p\), \(s \in L, |s| = 3p > p\).
• \(uvwxy = a^pb^pc^p\), \(|vwx| \leq p, vx \neq \epsilon\)
• Let \(i=2\)

• Case 1: \(vwx\) is entirely contained within \(a^p, b^p, \text{ or } c^p\).

  • Either v, x, or both must be made entirely of a’s, b’s, or c’s
  • Pumping that fragment results in more of that letter than the others, and the resulting string is not in the language

• Case 2: Either v or x falls on a boundary between letters

  • Pumping that fragment would result in a mixture of letters, and the resulting string is not in the language

• Case 3: v and x are made of two different letters (w falls on the boundary)

  • Pumping those fragments would result in less of the letter that did not contain v or x, and the resulting string is not in the language.

Ex 2

\(L = \{a^nb^na^n | n \geq 0\}\)

• \(p\)
• \(s = a^pb^pa^p\): \(s \in L, |s| = 3p > p\).
• \(uvwxy = a^pb^pa^p\): \(|vwx| \leq p, vx \neq \epsilon\)
• Let \(i=2\)

• Case 1: \(vwx\) is entirely contained within \(a^p\) or \(b^p\)

  • Either v, x, or both must be made entirely of a’s or b’s
  • Pumping that fragment results in more of that letter than the others, and the resulting string is not in the language

• Case 2: Either v or x falls on a boundary between letters

  • So v or x contains both a’s and b’s
  • Pumping that fragment would result in a mixture of letters, and the resulting string is not in the language

• Case 3: v and x are made of two different letters (w falls on the boundary)

  • Pumping those fragments would result in less a’s in the section that did not contain v or x, and the resulting string is not in the language.

Ex 3

\(\Sigma = \{0, 1\}; L = \{ww | w \in \Sigma^* \}\)

• \(p\)
• \(s = 0^p1^p0^p1^p\): \(s \in L, |s| = 4p > p\).
• \(uvwxy = 0^p1^p0^p1^p\): \(|vwx| \leq p, vx \neq \epsilon\)

• Case 1: \(vwx\) is entirely on one half of the string

  • Let \(i=2\)

  • By pumping, at least one symbol on the boundary is pushed over the boundary to the other half

    • Which means that either the second half would start with 1 (but the first starts with 0!)
    • Or the first half ends with 0 (but the second ends with 1!)

  • the resulting string is not in the language.

• Case 2: v and x are on opposite halves (w is on the boundary)

  • let \(i=0\)
  • The new string becomes \(0^p1^a0^b1^p\)
  • Both a and b cannot both be p, since either \(a < p\) or \(b < p\)
  • So the resulting string is not in the language

(…what about the boundary?)

Ex 4

(same language as ex 3)

\(\Sigma = \{a, b\}; D = \{ww | w \in \Sigma^* \}\)

Important note: CFL \(\cap\) CFL is not necessarily a CFL, but CFL \(\cap\) regular language is

Consider \(D' = D \cap L(a^*b^*a^*b^*) = \{a^nb^ma^nb^m | n, m \geq 0 \}\)

• Assume D is a CFL
• then D’ must be (since the intersection of a CFL and a regular language is a CFL)
• however D’ is not a CFL:
• \(p\)
• \(s = a^p b^p a^p b^p\): \(s \in L, |s| = 4p > p\).
• \(uvwxy = a^p b^p a^p b^p\): \(|vwx| \leq p, vx \neq \epsilon\)
• Let \(i=2\)

• Case 1: v or x crosses a boundary between a’s and b’s

  • By pumping this fragment, the resulting string introduces a mixture
  • no longer of the form \(a^nb^ma^nb^m\)

• Case 2: \(vwx\) is entirely contained within one section of a’s or b’s

  • By pumping this fragment, this changes the number of a’s or b’s on only one side
  • so the string is not longer in the language

• Case 3: v and x are made entirely of different letters (w contains the boundary)

  • Case 1: the boundary is the middle of the left section

    • By pumping this fragment, this changes the number of a’s, b’s, or both on only one side
    • so the string is not longer in the language

  • Case 2: the boundary is the center

    • By pumping this fragment, this changes the number of b’s on the left but not the right, a’s on the right but not the left, or both
    • so the string is not longer in the language

• so D is not a CFL.

Ex 5

\(\Sigma = \{a, b\}; L = \{x \in \Sigma^* | x \text{ is not of form } ww, w \in \Sigma^* \}\)

L is a CFL!

• Odd length strings are certainly not of this form

• what about even length ones? let \(L = a | b\), they must be the form \(L^n a L^m L^n b L^m\)

  • the (n+1)th symbol on the left is different from the (n+1)th symbol on the right
  • so at least 1 symbol must not match
  • note: \(L^n a L^m L^n b L^m = L^n a L^{m+n} b L^m = L^n a L^n L^m b L^m\)

S := A | B | A B | B A
A := L A L | a          # odd length strings with a in middle
B := L B L | b          # odd length strings with b in middle
L := a | b