Sets¶
10/5/2020 - 10/12/2020
Set: A collection of distinguishable objects, with unordered, non-repeating elements
Two sets are equal if their elements are equal
Notation¶
- \(z \in S\) - element member
- \(S = \{1, 2, 3\}\) - complete denotation
- \(\emptyset\) - empty set
- \(Z\) - integers
- \(R\) - real numbers
- \(N\) - natural numbers (no 0)
- \(Q\) - rational numbers
- \(A \subseteq B\) - all elements in A are in B (subset)
- \(\forall x, x \in A \to x \in B\)
- \(A \cap B\) - all elements in A and B (intersection)
- \(\{x: x \in A \land x \in B\}\)
- \(A \cup B\) - all elements in A or B (union)
- \(\{x: x \in A \lor x \in B\}\)
- \(A - B\) - all elements in A but not B (difference)
- \(\{x: x \in A \land x \notin B\}\)
- \(A \Delta B\) - all elements in exactly one set (symmetric difference)
- \(\{x: x \in (A - B) \lor x \in (B - A) \}\)
Given a universe of discourse \(\Omega\):
- \(\bar{A} = \Omega - A\) - all elements not in A (complement)
Demorgan’s Laws:
- \(\overline{A \cap B} = \bar{A} \cup \bar{B}\)
- \(\overline{A \cup B} = \bar{A} \cap \bar{B}\)
Definition:
- \(\{ x \in N | \frac{x}{2} \in N \}\) - even number definition by restricted comprehension
- \(\{ x | P(x) \}\) - unrestricted comprehension
Power Set: The set of all of a set’s subsets
Russel’s Paradox¶
Extraordinary Sets: All sets that include themselves as an element (ex. the set of everything that is not a teacup)
Ordinary Sets: All sets that don’t have themselves as a member
Paradox: Does the set of all ordinary sets contain itself?
This is a paradox - which means that the set of all sets cannot exist
Relations¶
Ex. \(<\) - the set of all ordered pairs \((a, b)\) s.t. \(a < b\)
- Cartesian product of 2 sets A, B: \(\{ (a, b) | a \in A \land b \in B \}\)
- e.g. \(\{c, d\} \times \{1, 2, 3\} = \{(c, 1), (c, 2), (c, 3), (d, 1), (d, 2), (d, 3)\}\)
Binary Relation
A binary relation on A and B is defined by some subset of \(A \times B\) - some examples of binary relations on \(N \times N\) are:
- \(=\): \(\{(1, 1), (2, 2), ...\}\)
- \(<\): \(\{(1, 2), (1, 3), (2, 3), ...\}\)
This can be denoted \(a < b \to (a, b) \in <\)
Properties¶
Note
For this notation, the symbol \(\sim\) represents an arbitrary relation. This can also be denoted \(R\), but that doesn’t look good in LaTeX.
- Reflexive: \(x \sim x\)
- ex: =, <=
- Symmetric: \(x \sim y \implies y \sim x\)
- ex: =, but not < or <=
- Transitive: \(x \sim y \land y \sim z \implies x \sim z\)
- ex: =, <, <=
- but not: \(\{ (x, y) | x, y \in N \land x = y - 1\}\)
If a relation has all 3 properties, it is called an equivalence relation
Functions¶
A function is a binary relation defined on the cross product of the domain and the codomain.
Given 2 sets A and B, a function \(f\) is a binary relation on \(A \times B\) s.t. for all x in A, there exists exactly one y in B s.t. \((x, y) \in f\)
Notation: \(f: A \to B\)
Graph¶
An undirected graph can be represented as a tuple \(G = (V, E)\) where V and E are sets (vertices, edges), where \(E \subseteq \{\{x, y\} | x, y \in V \land x \neq y\}\) (set of sets of two vertices)
A digraph is similar, but E must use ordered pairs rather than sets to indicate the direction of the edge, and an edge can go to the same vertex. \(E \subseteq \{(x, y) | x, y \in V \times V\}\)
Ex:
(1) --- (2) V = {1, 2, 3}
| E = {{1, 2}, {1, 3}}
(3)
(1) --> (2) V = {1, 2, 3}
^ E = {(1, 2), (3, 1)}
(3)
You can use digraphs to represent relations:
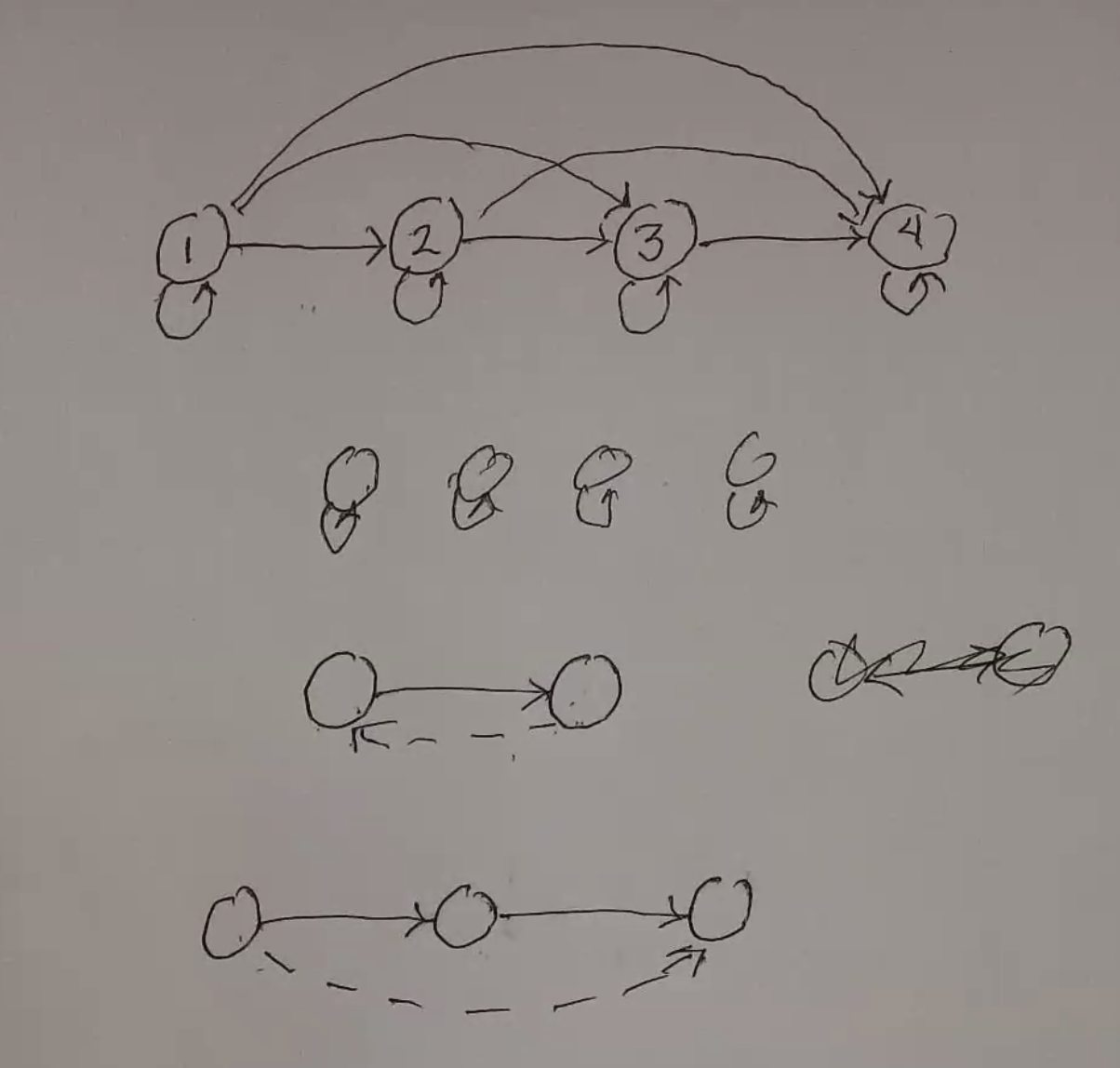
- Reflexive: every vertex has a self-loop
- Symmetric: all arrows must be bi-directional
- Transitive: the “jump” edge must exist (bottom of drawing)
Strings¶
Alphabet: Any finite set (usually notated \(\Sigma\))
A string over \(\Sigma\) is a finite length sequence of elements from \(\Sigma\)
The length of a string x \(|x|\) is the number of symbols in x
An empty string is a unique string of length 0, notated \(\epsilon\)
A symbol with an exponent (e.g. \(a^x\)) is repeated that many times
Note
\(a^0 = \epsilon\) and \(a^{m+1}=a^m a\)
\(\Sigma^*\) is the set of all strings over the alphabet \(\Sigma\)
Note
\(\emptyset^* = \{\epsilon\}\)
Propositional Logic¶
A proposition is a statement that is true or false.
Connectives
- not: \(\lnot\)
- and: \(\land\)
- or: \(\lor\)
- implies: \(\implies\)
- iff: \(\iff\)
Constants
- 0, 1 (false, true)
Variables
- \(X = \{P, Q, R, ...\}\)
Series of propositions/operations can be modeled using truth tables (which I am not going to write here, because tables in RST suck)
Tautology: A proposition that is true in any given state of the universe
Contradiction: A proposition that is false in any given state of the universe
Valid Argument: The conjunction of all givens and the negation of the output is false in all states.
e.g. given the argument:
P -> Q
P
---
Q
\((P \implies Q) \land P \land (\lnot Q)\) is always false.
Useful Tautologies¶
P -> Q P -> Q P -> Q P or Q
P not Q Q -> R not P
--- --- --- ---
Q not P P -> R Q
P
P P and Q Q
--- --- ---
P or Q Q P and Q
Cardinality¶
For finite sets, the cardinality of a set is the number of elements in the set.
Denoted, given a set A, \(|A|\). \(|\emptyset| = 0\)
For infinite sets:
- countably infinite: all elements in the set can be put in a 1-to-1 correspondence with natural numbers, or a list of the elements can be generated
- e.g. natural numbers (\(f(m) = m\))
- even integers (\(f(m) = 2m\))
- integers (\(f(m) = (-1)^m \lfloor \frac{m}{2} \rfloor\))
- strings over the alphabet \(\{0, 1\}\)
- rational numbers (map \(N \times N\) onto \(\frac{p}{q}\) by making a list)
- the union of any two countable sets
- strings over any finite alphabet
- uncountably infinite
- e.g. real numbers (diagonalization)
- set of all languages
Note
Let’s go back and look at \(\Sigma^*\) - all strings over an alphabet.
- \(\Sigma^*\) is countably infinite, but
- \(P(\Sigma^*)\) is not!
You can use diagonalization to prove that \(P(\Sigma^*)\) is uncountably infinite using the same binary argument as real numbers - use 1 to indicate an element’s presence in the subset, and 0 to indicate its not
In general, the power set of any set has greater cardinality than that set.